→ Logarithmes et Trigonométrie dans la ROM du HP 35

______________calculatrices________________

derrière les calculs rapides

le secret

des algorithmes

_________________________________________

Vous avez certainement déjà été frappés par la rapidité avec laquelle votre calculateur de poche trouve le logarithme d'un nombre ou le sinus d'un angle. Si vous avez quelques connaissances mathématiques, vous avez probablement pensé que la machine devait utiliser un quelconque développement limité ou une approximation polynomiale. En fait, la méthode employée est originale par rapport aux procédés classiques du calcul numérique et exploite des algorithmes en parfaite adéquation avec l'architecture de la machine. C'est à la découverte de ces «algorithmes machine» que nous vous invitons.

En 1972, la firme américaine Hewlett-Packard lançait le premier calculateur scientifique de poche jamais réalisé au monde le HP 35.

Ce merveilleux objet, qui possédait toutes les fonctions de base d'un ordinateur, était le résultat de la mise en oeuvre conjuguées d'une part des technologies microélectroniques de haute intégration (le HP 35 contenait dans quelques boîtiers l'équivalent de quelques 30000 transistors MOS) et d'autre part, des techniques parfaitement maîtrisées de la microprogrammation.

La taille de la machine était une contrainte sévère particulièrement pour la programmation des fonctions mathématiques complexes. En, effet, alors que les fonctions simples du type 1/x ou x² sont facilement obtenues en utilisant les quatre opérations de base, le cas des fonctions transcendantes et trigonométriques semble se heurter à l’obstacle insurmontable : le temps de traitement. Le lecteur dont les souvenirs mathématiques ne sont pas trop émoussés se souviendra de la lenteur de convergence d'un développement limité. Il remarquera, par ailleurs, que pour obtenir une précision suffisante le nombre de termes à calculer dans ce développement devra être important.

Il en sera de même pour un calcul sous la forme d’une approximation polynomiale (1). 0r, si des algorithmes utilisant ces principes sont parfaitement exploitables sur des machines de taille plus importante, une autre contrainte tenant à 1’architecture de la machine de poche existe.

En raison de la petite surface de la carte sur laquelle les circuits sont imprimés, l'appareil est organisé autour de trois bus série (Adresses IA, Instructions IS et sélection de champ WS).

Les informations formant le mot machine sont donc multiplexées dans le temps. Il existe même certains calculateurs pour lesquels les trois lignes de bus sont réunies en une seule, l’horloge de l'unité logique permettant seule de séparer les paquets d'informations. L'acquisition des données se fera donc bit à bit et leur sortie sera effectuée segment par segment sur les diodes électroluminescentes (2).

Le lecteur aura certainement remarqué qu’avec une telle architecture les circuits qui s’imposent pour l'unité logique et arithmétique, sont l’additionneur et le soustracteur série réalisés à l'aide de registres à décalage.

Les trois fonctions de base de l'unité arithmétique seront donc l'addition. la soustraction et le décalage. Il est fondamental de noter, à ce stade de l'explication, que l'algorithme réalisant les 4 opérations (+ − ÷ ×) en virgule flottante n'utilise rien d'autre que ces trois fonctions: la division des mantisses étant effectuée par soustraction décalage alors que le multiplication utilisera la méthode d'addition décalage.
 

La structure interne du calculateur de poche est donc particulièrement bien adaptée pour le calcul arithmétique en virgule flottante. Il peut, cependant sembler impossible de réaliser sur cette architecture et dans des mémoires mortes de faible taille des circuits d'évaluation rapide (quasi-simultanéité avec le pression d'une touche !) des fonctions mathématiques complexes.

C'est pourtant ce que réalisa l’ingénieur américain J. Volder en concevant pour une firme d'aéronautique un calculateur embarqué (airborne computer) capable de réaliser très rapidement sur une unité logique série, les calculs trigonométriques et logarithmiques de navigation.

Cordic (COordinate Rotation DIgital Computer), tel était son nom, est en quelque sorte l’ancêtre de nos HP 41 et autres TI 59.

Le principe de la méthode réside donc dans le fait que tous les calculs sont, pour respecter l'architecture de la machine, effectués à l’aide d'additions et de soustractions opérées sur des registres à décalages. Dans le cas d'un calculateur exploitant des données codées en DCB (décimal codé binaire) ce qui est notre cas (3) le mode angulaire choisi sera le radian. Ce choix est dicté par le principe de méthode.

Le lecteur remarquera que, moyennant que quelques constantes en MEM, tout calcul trigonométrique peut se ramener à celui de tangente d'un angle compris en 0 et π/4 radians, puisque :

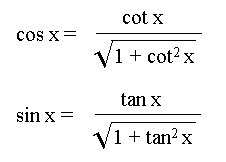
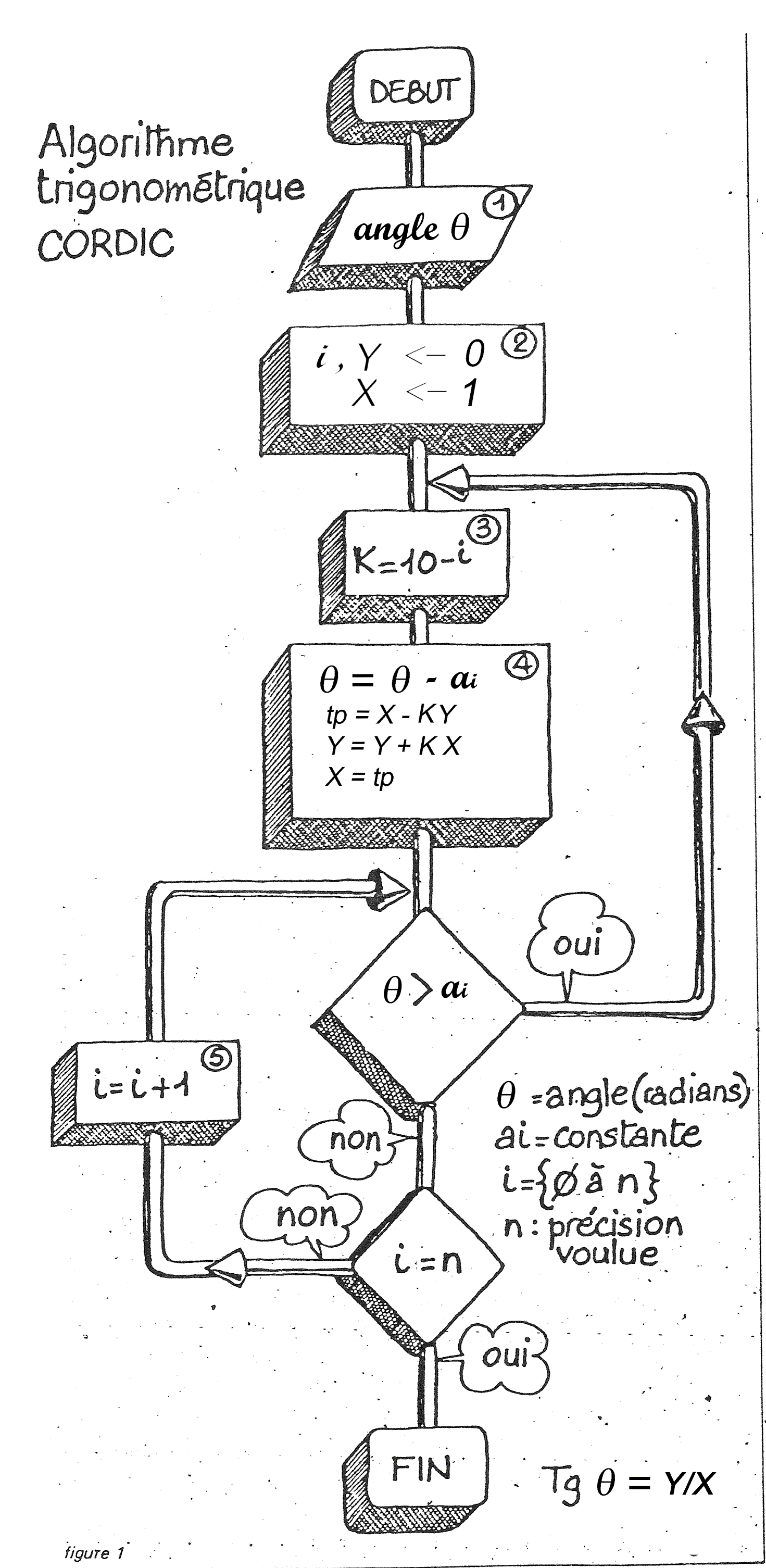
Un algorithme adapté à la structure de la machine

Les calculs seront agencés selon l'organigramme de la figure 1.

On remarquera que le processus consiste à soustraire à l’angle donné des contraintes, ai, en MEM, autant de fois qu’il est possible et de changer de contrainte dès que la soustraction ne peut plus être effectuée.

Ces contraintes - nommées ATR (arc tangent radix) - (pavé 4, fig. 1).


Pour un calcul en DCB, donc effectué en décimal, les constantes sont égales à :

a0 = tg^-1 1 = arctan (1) = π/4
a1 = tg^-1 0.1 = 0.0996686
a2 = tg^-1 0.01 = 0.0099996
a3 = tg^-1 0.001 = 0.001
a4 = tg^-1 0.0001 = 0.0001
et ai = 10^-i pour i suffisamment grand.

En étudiant de près l’organigramme, on s'aperçoit qui l’algorithme ressemble beaucoup à celui de la division. Il est donc parfaitement adapté à la conception « hardware » de la machine et ce fait à du jouer un rôle « miraculeux » pour son développement rapide.

 

La ligne trigonométrique est trouvée après quelques dizaines de boucles ainsi qu'on peut le constater dans l'exemple d'exécution du calcul de tangente x (figure 2)

Bien entendu, la méthode fonctionne dans l'autre sens et permet, en partant de la valeur de la tangente, de retrouver l'angle. La démonstration mathématique de la convergence de cet algorithme peut être trouvée dans l'article original de J. Volder.

Ce qui est étonnant c'est que ce principe peut s'appliquer à d'autres types de calculs parmi lesquels la recherche du logarithme d'un nombre.

Une impressionnante rapidité de convergence

La même rapidité de convergence et la même simplicité de structure se retrouve dans le processus de calcul du logarithme d'un nombre.

On peut noter, tout d'abord, que l'on peut, comme dans le cas des fonctions trigonométriques, se ramener à un problème type.

Le cas des logarithmes népériens est, en effet, le seul à considérer. Les logarithmes décimaux peuvent être fa­cilement  évalués  au  prix  du stockage d'une constante en MEM (4).

Cette valeur (ln 10) sera d'ailleurs utile pour le reste des calculs : log x  = ln x/ln 10 et 10^x = e ^{x ln l0} où ln est le logarithme népérien de base e.

Il faut, d'autre part, considérer que, de façon interne, les nombres sont toujours représentés en virgule flottante quel que soit le format réellement affiché.

On aura,  pour  le  nombre A=x×10^P, la relation suivante :

ln A = ln x + p × ln 10 (avec A>0).

On retrouve là aussi la constante ln 10.

Le seul cas finalement à considérer est celui de l'évaluation du loga­rithme népérien de x avec
1 ≤ x ≤ 10.

Les constantes préprogrammées sont les suivantes (5):

ln 10
ln 2  = ln (1+10⁰)
ln 1.1 = ln (1+10^-1)
ln 1.01 = ln (1+10^-2)
ln 1.001 = ln (1+10^-3)

etc. à la précision de la machine.

L'algorithme peut être schématisé comme indiqué dans l'exemple de calcul de ln x (figure 3 ci-dessous).

A chaque boucle, on multiplie le nombre Xi par une valeur ai sans que jamais le résultat n'excède 10. Si cela devait arriver, on change de constante ai dans l'ordre (2, 1.1, 1.01, 1.001 ...) etc.

Dans chaque boucle la soustraction de ln ai à ln 10 est opérée.

Le lecteur attentif aura remarqué que toutes les multiplications à effectuer peuvent toutes être, simplement et rapidement, réalisées à l'aide des opérations de décalage et d'addition, conformément au principe de la méthode.

La méthode de Volder peut s’appliquer à l'évaluation de nombreuses fonctions mathématiques telles que √x, tg n, ln x.

Elle peut également résoudre d'autres problèmes plus généraux, la conversion du binaire en décimal exemple

Pour le cas des machines de poche, notons que la programmation des algorithmes logarithmiques et trigonométriques permet d'obtenir facilement l'évaluation d'autres fonctions utiles au scientifique  P→R, R→ P, y^x (comme égale à e ^{x ln y}), etc.

Enfin, et ce n'est pas le moins surprenant, un certain Briggs (dans les années 1620 !) décrit une méthode dont s'inspire celle de Volder
(voir sur ce site l'article "Briggs and the HP35").

Ni l'ordinateur ni le calculateur de poche n'existaient alors. Il s’agissait d'optimiser le travail et d’économiser la peine des premiers calculateurs (humains) de tables numériques.

La prochaine fois que vous presserez la touche ln 
de votre HP 41 ou autre TI 59, peut-être vous sera-t-il amusant de penser que votre machine recalcule la table de logs, comme au bon vieux temps de Briggs et Néper !

 

Jacques LAPORTE
 

Notes

1 - A titre d'exemple, le développement suivant:
Sin x =  x  - x³/3 ! + x⁵ /5 ! ….
converge très lentement et il faudrait calculer un très grand nombre de termes pour avoir une bonne précision.

 2 - A titre de comparaison, on notera qu’un mot machine" d'un microprocesseur de type courant est de 8 bits (un octet) et que les transactions internes sont effectuée en parallèle. Le HP 35 exploitait quelques centaines de micro-instructions codées sur 10 bits.

 3. Dans le calculateur de poche, les calculs sont effectués chiffre par chiffre (1 chiffre = 4 bits) pour les raisons données plus haut. Ce fait lui confère une bonne précision mais une grande lenteur. Un nombre est stocké sur 8 octets dans la machine T159. A titre comparaison, un nombre en simple précision est stocké sur 4 octets en virgule flottant dans le langage' BASIC Il de Radio Shack ce qui permet la représentation des nombres jusqu'à + 1.701471 E+38 (TRS 80).

 4 - On notera que le logarithme décimal de 0.5 - par exemple. - n’est pas présenté sous la -forme classique 1. 698970004 mais comme égal à - 0.3010299957.

5- Cf fig. 2 les constantes « Cordic » réellement programmées dans la mémoire du calculateur Texas TI 59.

Bibliographie

J.E. VOLDER, “The Cordic Trigonometric Computing Technique”, IEEE Transactions on Electronic Computers, Sept. 1959,

A. DELEDICQ et P. VASCALDE, “Le calculateur programmable de poche » CEDIC 1978 et particulièrement les pages 112 à 115,

J.M SMITH, « Méthodes Numériques  pour Calculateur de Poche », Eyrolles, 1975 (et particulièrement les pages 38 à 42),

« Texas Instruments Software Exchange Newsletter » Vol II  n°2 et 3.

___________________________________________________________________________________________________

Cet article a été publié, pour la première fois, dans le numéro 24 (Février 1981) de la revue l’Ordinateur Individuel.

C’est le texte original que nous republions ici, correction faite de quelques typos, dans l'organigramme ajouté par le journal.

L'article de Jack Volder (1959) mérite une lecture attentive, nous en donnons le PDF à titre pédagogique.

L'approche de Volder a été généralisée par J.S. Walther de HP en 1971 et dans son article (PDF en download), l'algorithme général est appliqué à de nombreuses autres fonctions : Walther, J.S., “A unified algorithm for elementary functions,” Spring Joint Computer Conf., 1971, proc., pp379-385

Jack Volder fit un premier rapport interne (chez Convair) au sujet de CORDIC in 1956 et en 1959 il publia l’article final dans les “Proceedings of the Western Joint Computer Conference”. Volder quitta Convair avant que le premier prototype soit construit par la firme.

Il mit sur pied son propre démonstrateur avec l’aide d’un associé nommé Macmillan. Tous deux arrivèrent à le présenter à HP  (Bill Hewlett lui-même?) durant l’été 1965.

Les gens de HP devaient se souvenir du concept lorsque la firme démarra le projet de son premier calculateur scientifique de table : le HP 9100A.

Osborne (un consultant indépendant) qui fut un des artisans principaux du hardware du HP 9100 fit équipe avec David Cochran (un ingénieur de HP) pour le «firmware».

C’est Volder lui-même qui fit connaître à Cochran les concepts de “pseudo multiplication” et de “pseudo division” décrit pour IBM par J. E. Meggitt et publiés en 1962.

Pour la ROM du 9100, Cochran utilisa l’algorithme de Volder pour les fonctions trigonométriques et celui de Meggitt pour le calcul des logarithmes, exponentielles, et racine carrée. Pour la ROM du HP35, c'est l'implémentation du Cordic par Meggitt qui est utilisée ; on reconnaît l'approche en deux parties "pseudo division" puis "pseudo multiplication" et le choix des constantes. Voir pour plus de détails mes articles commentant pas à pas la ROM du HP35.

Les deux approches sont cousines: elles n’utilisent que des opérations de décalage et d’adition.

Les ingrédients de base pour cuisiner la Rom du HP35 étaient sur la table.

Cf. J.E. MEGGIT, Pseudo Division and Pseudo Multiplication processes, IBM Journal, Res & Dev, April 1062, 210-226 et en particulier p. 224, pour l'implémentation du Cordic sur un calculateur DCB.

___________________________________________________________________________________________________

Pour plus de pédagogie, j’avais traduit en langage ‘C’ l’organigramme de la figure 1.
La compilation est immédiate: gcc cordic.c
Mais il est plus intéressant maintenant d'étudier Cordic -pas à pas- en utilisant le simulateur de la ROM du HP 35: The HP-35 Microcode Simulator

_________________________________________________________________________________________________

Je signale l'intéressante recherche de Noël Jouenne sur les calculatrices électroniques de poche dans l'optique d'une ethnologie des techniques : "je m'intéresse plus à l'utilisation et à l'utilisateur qu'à la machine elle-même. Pour l'heure, cette recherche n'en est qu'à son début, et je ne présente dans ces pages que des documents pouvant être utilisés par le lecteur pour assouvir sa propre curiosité".

On peut trouver de bonnes présentations formelles de l'algorithme en français, sur le site Trigofacile ainsi que sur le site de Olivier Rochoir.

En Anglais, le :  CORDIC FAQ de Grant R. Griffin est excellent ; mais rien ne vaut de lire les articles originaux de VOLDER, MEGGIT et WALTHER (cf. ci-dessus).