HP 35 Logarithm Algorithm
The algorithm used by D. COCHRAN for the HP35 log routine (see a quick summary in my article “The Secret of the Algorithms”) is directly derived from J.E. MEGGITT (1) who described in his paper “digit-by-digit methods for the evaluation of the elementary functions” globally named “Pseudo Division and Pseudo Multiplication Processes”.
The article’s abstract outlines that these methods “involve processes that resemble repeated-addition multiplication and repeated subtraction division. Consequently, the methods are easy to implement and the resultant execution times are short.”
In fact, the HP designer found there all what he needed: an operation process on BCD digits using “shift and add” only.
Here is a formal presentation of the maths involved
under the hood of the machine’s ROM (see here ROM listing).
Afterwards, I’ll show, step by step how calculations are performed.
(All notations and calculations are made using Mathematica).
First, two simple simplifications:
1- We will consider only the natural logarithm ln(x)
since we have log10(x) = ln(x)/ln(10) ; we just need the constant ln(10) in
ROM.
2- The only case to consider is the normalized mantissa ( .xxxxxx ) since by
general logarithms definition:
ln(M 10k) = ln(M) + K ln(10)
There again we need the ln(10) constant.
The heart of the approach is essentially similar to
BRIGG’s method, slightly modified though to save accuracy during iterative
processes.
We search ln(M) and we consider a number formed by the product of small
quantities ![]() in
which
in
which ![]() is a
small real number and
is a
small real number and ![]() an
integer exponent.
an
integer exponent.
Formally we have:
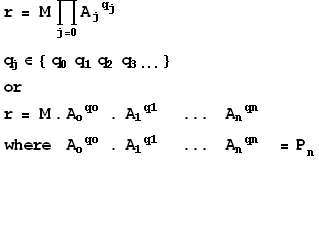
so shortly written ![]() .
.
We can select each factor ![]() in
order to drive r close to 1.
in
order to drive r close to 1.
To the limit, the expression ![]() can
be written
can
be written ![]() and have:
and have:
ln(M) + ln(Pn) = 0 and
ln(M) = - ln(Pn).
In practice though, the
![]() limited
in numbers and
limited
in numbers and
ln(M) = ln(r) – ln(Pn) r being a very
small remainder.
We can take as Briggs did (golden rule) :
![]()
and finally
![]() .
.
We need now to take into account the specificity of the HP 35’s A&R: no multiplication, only addition and shifting operations.
There we have a fit (quite miraculous): the Meggitt’s approach (like Volder’s) requires precisely add and shift only.
1) First optimization
We need to find a way to reduce computation time and
amount of ROM required by constants.
Meggitt proposes for ![]() the
form (1 + 10-j) ;
the
form (1 + 10-j) ;
That is to say:
![]() etc.
etc.
In the ROM we find effectively: ln(10), ln(2), part of ln(1.01), of ln(1.001)
etc.
For some constants, in fact, the code computes simply part of the number (leading patterns) and loads from ROM only non regular patterns too odd to be computed {330985 for ln(1.01) etc} ; see trace and ROM listing for details.
2) Algorithm core.
Driving the product M Pn (or ![]() )
close to 1 means to multiply intermediate result MPn-1 by a number (1+10-j)
)
close to 1 means to multiply intermediate result MPn-1 by a number (1+10-j) ![]() times,
times, ![]() being
the largest integer exponent such that the product M Pn goes closer to 1 each
time but keeps < 1.
being
the largest integer exponent such that the product M Pn goes closer to 1 each
time but keeps < 1.
This operation is a pseudo multiplication using adding
and shifting since ![]() are
of the form 1.00….1 (eg M 1.01 requires shifting M 2 times to the right and an
adding the result to M).
are
of the form 1.00….1 (eg M 1.01 requires shifting M 2 times to the right and an
adding the result to M).
When Pj is > 1, the algorithm must change constant ![]() and
increment the exponent j in (1 + 10-j).
and
increment the exponent j in (1 + 10-j).
Here are the 6 constants used by the HP35, on a 56 bits register, though the method is quite general.
J ![]()
0 (1 + 10-0)
= 2
1 (1 + 10-1)
= 1.1
2 (1 + 10-2)
= 1.01
3 (1 + 10-3)
= 1.001
4 (1 + 10-4)
= 1.0001
5 (1 + 10-5)
= 1.00001
An intermediate calculation step is done simply by
shifting the previous result to the right qj times and adding the result to the
previous intermediate value![]() :
:
![]() eq1
eq1
Let take an example (the same as in my main article):
ln(4.4) (for a mantissa M in the range
0 < M < 10 (note that we just need constant ln(10) to adjust range):
(1+10-j) ![]() =
M(1+10-j)
=
M(1+10-j)
| 4.40000000000000000000 | 2.00000000000000000000 | 8.80000000000000000000 |
| 8.80000000000000000000 | 1.10000000000000000000 | 9.68000000000000000000 |
| 9.68000000000000000000 | 1.01000000000000000000 | 9.77680000000000000000 |
| 9.77680000000000000000 | 1.01000000000000000000 | 9.87456800000000000000 |
| 9.87456800000000000000 | 1.01000000000000000000 | 9.97331368000000000000 |
| 9.97331368000000000000 | 1.00100000000000000000 | 9.98328699368000000000 |
| 9.98328699368000000000 | 1.00100000000000000000 | 9.99327028067368000000 |
| 9.99327028067368000000 | 1.00010000000000000000 | 9.99426960770175000000 |
| 9.99426960770175000000 | 1.00010000000000000000 | 9.99526903466252000000 |
| 9.99526903466252000000 | 1.00010000000000000000 | 9.99626856156599000000 |
| 9.99626856156599000000 | 1.00010000000000000000 | 9.99726818842214000000 |
| 9.99726818842214000000 | 1.00010000000000000000 | 9.99826791524098000000 |
| 9.99826791524098000000 | 1.00010000000000000000 | 9.99926774203251000000 |
| 9.99926774203251000000 | 1.00001000000000000000 | 9.99936773470993000000 |
| 9.99936773470993000000 | 1.00001000000000000000 | 9.99946772838728000000 |
| 9.99946772838728000000 | 1.00001000000000000000 | 9.99956772306456000000 |
| 9.99956772306456000000 | 1.00001000000000000000 | 9.99966771874179000000 |
| 9.99966771874179000000 | 1.00001000000000000000 | 9.99976771541898000000 |
| 9.99976771541898000000 | 1.00001000000000000000 | 9.99986771309614000000 |
| 9.99986771309614000000 | 1.00001000000000000000 | 9.99996771177327000000 |
j = 0
j = 1
j = 2
j = 3
j = 4
J = 5
At each line a test to < 1 is made; if not < 1 (eg 1.1, 2 times) the constant is changed (eg 1.01 instead of 1.1).
Let us take another example to show the
pseudo-multiplication process.
We want to compute 0.968 (1.01)3
on a CPU without multiplication and power function.
We shift 0.968 2 times to the right: 0.968 -> 0.00968
Then we add the 2 numbers; the intermediate value is 0.97768 at the first step.
There we follow eq1 ![]() and
we have: 0.97768 = 0.968 * 1.01.
and
we have: 0.97768 = 0.968 * 1.01.
We need 2 more steps since exponent qj = 3.
Second step, the shifted value is 0.0097768 and intermediate 0.9874568,
third and last step gives 0.009874568 and finally 0.997331368.
This pseudo multiplication process is the same used by
Jack VOLDER in CORDIC algorithm, for trigonometric.
Let’s get things together:
1- operation ![]() is
done using only adder and right shifter,
is
done using only adder and right shifter,
2- at each intermediate step, a test to 1 is made. If intermediate result
exceeds 1, we skip the result and take the next constant.
This iterative process leads, in the case of 5 constants which is consistent
with the HP35 precision, to a result which is –in our example ln(4.4)- a set of
exponents ![]() = {7,
6, 2, 3, 1, 1} which are the “pseudo quotients” in the process.
= {7,
6, 2, 3, 1, 1} which are the “pseudo quotients” in the process.
This is the end of part one in the Meggitt’s algorithm, reading 1.00001 is applied 7 times, 1.0001 applied 6 times etc…
The pseudo multiplication is “identical to an ordinary multiplier save that the multiplicand is set from some read-only store to the required value » Meggitt op. cit. p.215.
To find the ln(4.4) we just have to substract from ln(10), 7 times ln(1.00001), 6 times ln(1.0001), 2 times ln(1.001), 3 times ln(1.01), 1 time ln(1.1) and finally 1 time ln(2).
We have though to take care that forming
r = M 21 1.11 1.013 1.0012 1.00016 1.000011
- the remainder r is driven to 10 instead of 1 as
neaded (the argument's range is 0<M<10) : a division by 10 will align the
remainder),
- we have to take into account this small remainder ; which is in our case 0.00000322882267342 (10 –
9.99996771177327000000)/10
(below, the first line is the remainder, the 6 next lines
corresponds constants ![]() j
times each )
j
times each )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and the rest is straightforward:
(10-p)/10 + 7 ln(1.00001) + 6 ln(1.0001) etc… =
![]()
and the result is (ln(10) – previous line) :
ln(4.4) =
![]()
________________________________
(1) J.E. MEGGITT, Pseudo Division and Pseudo Multiplication processes, IBM
Journal, Res & Dev, April 1962, 210-226.