HP35 trigonometric algorithm

I first met CORDIC in the 70’s, working as a technical journalist on the first hand held calculators.

My investigations led me in the world of airborne computing and in fact the two fields had a lot in common: no time to lose (you must do this calculation right now and here at your fingers!), no room to stuck a big arithmetic unit, no big ROM to store complex algorithms and no much RAM at that time.

I was not surprised therefore to learn that the HP9100 and HP35’s software architects were in touch with the man at Convair, Fort Worth Texas who worked on the navigation software of the B-58A Huster (first USAF supersonic operational bomber) : Jack Volder.

Volder published his work in 1959, quit Convair, built a prototype and managed to show it to HP. 

In 1965 Hewlett Packard was ready to launch its HP 9100A project (HP’s first desktop programmable scientific computer) and the rest of the story is quite an industrial miracle, a miracle driven by an incomparable visionary: Bill Hewlett.

A team was built and David Cochran received the charge (or the burden) to bootstrap trigonometric algorithms in the HP 9100’s tiny ROM.

Volder showed him the remarkable work of IBM’s Meggitt and the vast potential of this wide class of pseudo multiplication-pseudo division algorithms.

The HP 9100’s project just finished (“About 15 minutes-or-so after  ..“), Hewlett wanted more, for a new calculator: “we should have one in a tenth the volume, ten times as fast, and at a tenth the price” and “You ought to be able to put it in your pocket “, he added later.

Then again, Cochran did a remarkable job; piling up in a small piece of silicium, an astonishing sum of software engineering.

1) A simple presentation of CORDIC.

There are a lot of brilliant formal presentations of CORDIC, nowadays.
 

I will focus first on the way Volder discovered how to design his “digital computer for real time airborne computation”, which he described “not based on the conventional pencil and paper computing techniques”. Afterward I will present Cordic in its HP35's implementation.

At the time of my research, Volder was said to have been inspired by his handbook of “Chemistry and Physics”. If this is true (1), he certainly had found there some kind of rather basic trigonometric equations and among them the formula for the rotation of a vector in a coordinate system (angle is counter clock-wise):

                  eq1

It does not take much time to discover the CORDIC trick.

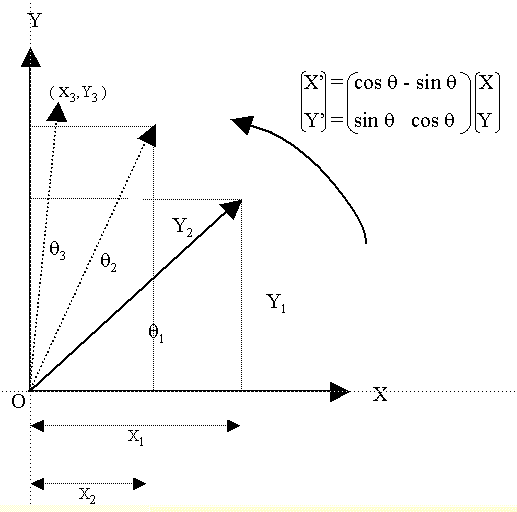
Volder was searching an additive way to calculate any tan θ (Y/X) with a set of known constants. 

We start with a known angle θ = 45° (tan θ = 1), and we calculate a first rotation θ2 (Y2/X2) with the equations rearranged by dividing both sides by cos θ.

A tangent term appears.

We have now:

 and                     eq2

we can neglect the scaling parameter  since we are interested only in the ratio  which is the tangent of the angle  plus the additional rotation angle  :

.

It is clear that the rotation expressed by equations 1 and 2 is doing the trick: the tangent of any angle can be found, operating on smaller angles whose sum equals the large one.
So, if we break an angle into smaller angles whose tangents are known, the goal is won.

Let’s clarify the point by a numerical example.

We want to compute tangent of the angle made by vector (X3,Y3 ) and the x axis: that is to say the angle θ1 + θ2 + θ3  : 85° = 45° + 20° + 20°.

The angle being reduced to zero, we start from vector X1=1, Y1=0 and make a rotation of θ1=45°.  We apply therefore equation 2 and the result is X2 = 1 and Y2 =1.

We continue with the new values (X2 = 1 and Y2 =1, θ2=20°) for a second rotation and the result is (X3 = , Y3= ) ; for the third (also 20°) we have a final result of X4= ,Y4=,  and the ratio Y4/X4 = which is in fact tan(85° = 45° + 20° + 20°).

It turns out that if we can reduce an angle θ to a sum of known tan-j (arc tan), we are on a good track:

At the end of the calculations, there is a very small remainder r.

There we meet something we already know! It is the pseudo-division operation we have met in the logarithm algorithm and  are the pseudo quotients (the number of subtractions possible for a small angle).

To compute tan(θ) we “just have” to break θ  into a sum of smaller angles whose tangents are known, keeping tracks of the numbers of subtractions. Then using the very small remainder (more on this later) we’ll apply the rotations equations (eq2),  times for each angle.

I must take a pause here to explain the HP35 algorithm designer’s point of view versus Volder’s point of view.

CORDIC is a binary computer (hardware architecture) while the HP35 ROM is software for a BCD shift and add only arithmetic unit. That is why D. Cochran implemented, in fact, the Meggitt’s version of the Cordic: the pseudo division, pseudo multiplication approach (2).

Another major consequence of this, is the choice of the factors ; since we have to restrict ourselves to add and shift operations, will simply be powers of 10 (1, 0.1, 0.01, 0.001  ...) then the rotation formulas are simply:

  eq2

Trigonometric and logarithm algorithm are so closed that we are sure to be able to reuse some “cousin” routines!

A third point to be discussed here is the angle mode to be chosen.
Since the constants to be stored in ROM are  the designer made the choice of radian mode for calculations since the “patterns” to store requires much less room than in the degree ( tan-1(0.01)= 0.00999966, tan-1 (0.001)=0.00099999, tan-1 (0.0001)=0.00010 etc…).

 2) Calculation prologue.

All calculations will be done in radians while angles are supposed to be entered in degrees (there is no way to set up the angle mode of the HP35).

The conversion is done using the formula. 

To be coherent with my previous article “The secret of the algorithms”, I have chosen the same example tan(1.5 radians), requiring to feed the simulator with an angle of  85.943669260 degrees.

The trace capture is based on this argument.

From the start of the trace (label disp5) to the start of the trigonometric algorithm, we are looping in the “wait a key” routine. Here are a few details but I will comment all the service routines later.

From [CP0] to [CP0a], control is idling waiting for any key stroke. It occurs at [CP0a] and status flag 0 is raised by hardware (be careful S=0.....678..b means flags 0, 6, 7, 8 and 11 are ON (bit=1) others are OFF (bit=0).

Now we enter in a “long” loop (about 14.4 msec, 48 word times), just to prevent key bounce from executing a function twice (pointer p is decremented from its starting value Hex C=12).

We are now at [CP0b], display is turned off and we test if a key is being processed at that time (S8 = 0) to insure one key is processed only once. It is not the case, so we branch to the key “Tan” address: 00050, where we met switch corresponding to different cases (S1 ON is trigonometric lines S1 OFF is square root, S10 ON is Arc while OFF is direct lines etc...).

At [CP0c] some preparations take place: number 90 is entered in C register C=09000000000001 (we’ll see why little bit later) and, in the case of Tan (S1=ON), we are calling the divide subroutine to make θ/90, first step of the conversion degree to radian mode (next step is multiplication by).

Finally, at address 02270 [CP1], we enter in the tangent core algorithm, with the angle in radians; A register is the angle value 08594366926001, while B has the mask: 09000000000000.

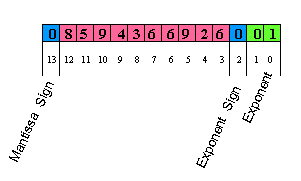
Note that, data in register A is in the regular format, the number 85.94366926 being represented by:

- mantissa sign “+”: digit 13=0,
- mantissa: digits 12 to 3: 8594366926,
- exponent sign “+”: digit 2=0,
- exponent : digits 1 and 0= 00.

From [CP2] to [CP3] we are computing angle/90 using the division floating point routine (to be commented in upcoming article).

The reason to do this is simple. Only one “pi” related constant is stored in Rom (to spare room): ; thus, to compute , we have to divide the angle by 90 and then multiply by .

At [CP4] (call to routine atc1) the constant  is added to itself (address 01164) to have; the multiplication takes place and at address 01166 finally than angle is expressed in radians (A=01500000000000, θ =1.5 radians).

Following the process,  is loaded once again and added to itself to have finally.  We are at [CP5] and scaling (pre21) can begin (address 01173).

The reason of this “scaling” process is simple: the angle must be scaled to be ; to speed calculation, repeated subtractions of factor  are done in floating point:

-  is repeatedly subtracted from until the result is negative,
- then we go one step backwards,
- the remainder is ,
- next step, the remainder is expressed as and is  repeatedly subtracted,
- the process is repeated until exponent n is zero.

The process is not clear with a small angle like 1.5 radians, so I give another “pre21” example, resolving a big angle: 320 radians.

We are now at [CP6], angle is converted in radians, and we need to load the first constant of:

 
that is to say to compute the first pseudo quotient.

2) Pseudo division

At [CP7], the first pseudo-division (label pqo16) is calculated, subtracting B=00785398163500 from A=00714601836500 (a - b -> a[w]) as many times as possible, until there is a carry.

The result is stored at byte 13 of C register (pqo15): C=10000000000000 (c + 1 -> c[s]).

At [CP8] the next constant is loaded : 0.09966865249 and the second pseudo division takes place, giving  pseudo quotient equal to 7, and so on.  

The later constants are more simple = 0.00999966669 etc justifying the choice of radian mode.

During the calculations of, leading zero digits are generated in the resulting angle remainder.

To save accuracy by preserving significant digits, the remainder is shifted left one digit during each pseudo-quotient calculation (decade) (at label pqo11 address 01234).

Finally all is done at [CP9] and the result is 96171 and the remainder is  which comes out in register A, as  (effect of accuracy saving shift left on a 5 digit long pseudo-quotient).

The steps of the pseudo division process are given below, using Mathematica, to ease reading the trace file:

3) Pseudo multiplication

We are ready now to calculate tan(θ) applying the Cordic rules:

-using rotation equations:

-starting from X=1 and Y= (for very small angles:)

The first step of computed with Mathematica is:

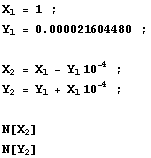
But we have to rewrite a little our equations since “as is” implementation will lead to an expensive 4 register scheme (we must keep shifted values in each equation (X and Y) to subtract or add to the non shifted previous ones).

We simple have to use a third value, say Z, and write  where j starts from 4 in the case of 5 digit pseudo-quotient (3).

That leads to a new set of equations (replacing  by its new form, and multiplying both sides of the second equations by):

where  is the new and  the new Z.

There is nothing magical is this transformation but it’s simply a transformation of mathematical expression for hardware implementation.

Let’s clarify this point:

If we want to form Y+X 0.01 with
X=3.14159
Y=2.71828
we can shift X = 0.0314159 then add both numbers Y+X 0.01=2.74969
or we can let X=3.14159, and multiply Y by 100 and add X + 271.828=274.969,
we have the same digits (the place of decimal point has to be corrected).

In the case of our 2 equations, this method is more economical (we use 3 registers, instead of 4).

Implementing this directly in the ROM is a little tricky. Register A holds X, C holds Z, while B has the shifted for of Z ().

You’ll have to study the trace carefully at [CP10]:
- the sign byte of A is use to keep, that is to say, the number of times we have to apply this rotation of angle  (9 times),
- the sign byte of register B holds the indices j (starting from 4 to 0)
- while sign byte of C is holding the number of double shift right to apply to register B, to implement operation : in this case 4 times 2 SR (label tan18).

Finally, (address 01360, 01361), the new Z is calculated and the new X:

01360:             a + c -> c[wp]
  A=80009999999999  B=40000000000021  C=90012160434443
  D=56171000000000  M=00000000000000  P=c  S=01....678..b

01361:             a - b -> a[wp]

  A=80009999999978  B=40000000000021  C=90012160434443
  D=56171000000000  M=00000000000000  P=c  S=01....678..b

Note that the stack is used (at 01374) destroying thus its top.

At [CP11] (01361), we apply the 4th rotation, for the first time, we have the following result (A and C, correctly aligned values): and.

The rest of pseudo multiplication calculation is a repetition of that scheme for others rotations.

At [CP12], the calculation is finished:

A=01460742161998,
C=01035883033997.

The rest of tangent generation is a call to the floating-point division to make A/C, leading to a result in normalized form: C= 01410141989001 [CP13], and in [CP14] the mask in B is built allowing the display (tan(θ)= 14.10141989).

Please, study in the trace the role of system flag 9, at address 01006:

01006:                         if s9 = 0
01007:                         then go to tan16
01010:                         a exchange c[w]
01011:  tan16:              if s5 = 0
01012:                         then go to asn12
01013:                         0 -> c[s]
01014:                         jsb div11

Depending on the state of flag S9, we take another path and registers A and C are swapped. The reason is simple:

- A is always divided by C to use the same code, but factors signification is changed,
- if we press the TAN key, S5 is OFF and A/C gives tan(θ), but if we press the COS key S5 is ON and register A and C are exchanged, so that dividing A/C, we compute cot(θ).

If fact we have only two routes, since sin(x) is calculated with tan(θ) using:

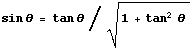
and cos(x) is calculated with cot(θ) using:

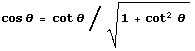
( is calculated as )

You can download a trace for cos(x), roughly commented; I will detailed the floating point multiplication and square routines later, on these pages.

Enjoy and please, give me feedback.
06 December 2005

(1) Jack VOLDER confirmed this point in his recent paper "The Birth of CORDIC", Journal of VLSI Signal Processing 25, 101-105, 2000.
(2) J.E. MEGGIT, Pseudo Division and Pseudo Multiplication processes, IBM Journal, Res & Dev, April 1062, 210-226. See trigonometry functions p.225.
(3) Cochran implemented here closely the Meggit's approach ; see his paper p. 224.