Henry Briggs and the HP35
I will start this article with a few words about Henry Briggs himself (1561-1630) who published in 1624 his book “Arithmetica Logaritmica” [1], describing a set of methods to help calculate tables of (common) logarithms.
Napier (or Neper) (1550-1617) is the inventor of the logarithms around 1614 ; Briggs and Napier agreed to redefine logarithms so they have 10 for base (what we call today “common logarithms”).
 In
the following years Briggs published “common logarithms” tables and the method
to compute them.
In
the following years Briggs published “common logarithms” tables and the method
to compute them.
In fact, these base 10 logarithms tables were still in use in the 70s and the slide rule (which is a direct application of logarithms) was at this time a common engineer tool.
I have already explained how Hewlett-Packard with its HP35, introduced in 1972, revolutionized the engineering world.
No more logarithm tables or slide rule to handle. Just press a key.
I remember that time (the start of my career) and the day I put my fingers on a HP35. Immediately, I pressed ln(x) and magically the result was there in around 200 ms!
Surprisingly, the internal algorithm was said to be based on a method close to the approach that described Briggs in 1624!
The present article is about the link -somewhat magical- between Briggs and the HP35.
Briggs’ book is available on the Internet (in English) on the Ian Bruce’site University of Adelaide, Australia.
Briggs “Golden rule”
Briggs organized his work in a simple way; genial ways are often simples.
A left column was supposed to contain the numbers (“numbers from continued means from 10 to 1”) while in a right column he would write their logarithms.
He started with 10 and log(10)=1.
Then he calculated repeated square roots of 10 and in the right column he place the half of the preceding number: log (√ n) = (log n) / 2.
I reproduced here the table from Briggs’s book.

Briggs did those calculations down to the 54th root of ten.
The result is very close to 1:
1.0000 00000 00000 01278191493 etc
And the logarithm (base 10) is:
0.00000 00000 00000 0555111512
Then he made his discovery of the “golden rule”.
Considering the “significant figures” (notae significativae) of the numbers:
first:
127819149320032
second:
555111512312578
third:
1
and finally X the logarithm to be found.
Briggs wrote (Chapter 6, p 12): “I assert that these four numbers are in proportion” and he computed the fourth X applying the ratio to number 555111512312578.
The result 434294481903251 is the significant part of the logarithm of our third number:
X =
log(1.0000,00000,00000,01) = 0.00000,00000,00000,04342,94481,90325
Briggs saw clearly the role this constant [Ch 6, p.12]: “hic autem sola multiplicatione totum negotium absovit” (“by multiplication alone the whole work is done”).
To show clearly the computation process, let us seek log(6) by the Brigg’ s method (Arithmetica Logarithmica Chapter 6) but with a tool he could not imagine.
I will use Mathematica to do the hard core calculations.
Let's calculate “continued means” for the case of log(6) (successive square root of 6 between 50 and 53):
![]()
![]()
![]()
![]()
Then we have:
![]() =
=
![]()
and –as Briggs did (Chapter 7, for the calculation of log(2)) – let’s write the four numbers in proportion:
1
1989252617
Notae Mediorum ut
prius
4342944819
Notae Logarithmorum ut prius
8639214348
the fourth number is found by the golden rule “per proportionis illam auream regulam”:
![]()
and the final result is (log 6)
![]()
One important point is:
If I take the log calculated by “golden rule” I have (shorter writing):
8.6392 10-17 * 253 = 0.77815… = log(6)
but if I take the “continued means” minus 1:
1.9892 10-16 * 253 = 1.791759…= ln(6).
By the Briggs’ method, we find the log to base 10, by finding first the natural log (ln(x)) (!) as the HP35 calculates first and always the natural log.
For each value in
the “continued means” column, he computes![]() , but we must keep in mind that, if k is high (e.g. k=53):
, but we must keep in mind that, if k is high (e.g. k=53):
![]()
HP35 Golden rules
Knowing –already- a few rationale logarithms, log(10) … Briggs showed us how to find log(x) –in fact ln(x)- by a so called golden rule.
HP35 had in its ROM the code of a very similar golden rule!
Let’s get things together.
The search for this “proportionality zone” is the key of Briggs’ method, and also of the HP 35’s algorithm.
If we go down the square root list, there is a rank k for which the roots and the logs are in proportion: rn+1 / rn ~ ½ and ln+1 / ln = ½.
There is an optimal rank where the number of leading zeros and of significant digits is almost the same; going further will only reduce significant digits numbers.
Now, if like Briggs,
at the rank k, we consider ln(1+rk), we can say there is an
interesting proportionality:
ln(1+rk) ~ rk e.g. ln(1.000005) ~ 0.000005, the
natural log being proportional to ln(10): rn / ln
= ln(10).
What Briggs called “golden rule” is in fact the effect of the higher terms of
the power series expansion of ln(1+rk) compared to the significant
figures considered:
![]()
![]()
the difference being very small for 5 leading zeros:
![]()
![]()
In fact, the HP35
Rom follows exactly this scheme (the algorithm is due to
J. E. Meggitt
[2]) : for lower exponents it has
constants ln(2), ln(1.1), ln(1.01), ln (1.001)) but ends calculation
using Briggs’ approximation ln(x) ~ x-1.
For ln(x) the HP35-Meggitt’s algorithm is directly derived of what is explained
above (x between 0 and 10); let’s write:
![]()
The first part of
computation time is spent to seek the set of ![]() parameters
(pseudo division), each one larger as possible, the product
respecting the inequality.
parameters
(pseudo division), each one larger as possible, the product
respecting the inequality.
All calculations
here are simply a question of additions and right shifting, for example
multiplying x by 1.1 is simply shifting BCD value of x right then adding it to
itself (see my article about ln(x) trace on the HP35).
Second part, (pseudo multiplication) the natural logarithm we search is
simply a question of subtractions, using the set of parameters ![]() we
have computed so far.
we
have computed so far.
For ln(6) the HP35 computation of the set of ![]() gives
053442, where 0 is q0, 5 is q4, 3 is q3
etc.
gives
053442, where 0 is q0, 5 is q4, 3 is q3
etc.
The product p above:
![]()
leads to expression
of ln(x):
![]()
and with Brigss’ approximation ln(a) = a -1
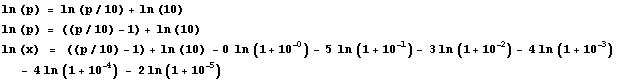
Factors
![]() and
and
![]() are
listed below:
are
listed below:
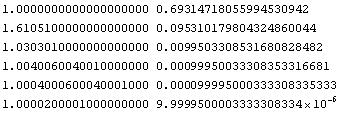
Product p is
![]() and
the result ln(6) is
and
the result ln(6) is
![]() .
.
In fact the machine was not so accurate!
350 years later …
Here is how can be summarized –in his words- the discovery of Henry Briggs:
t being small, that is to say the number of root extraction is high (54th for 10), there is a proportionality “golden rule”, that can be written as
log(1+t) ~ 0.43429448… t
or E / (D-1) ~ 0.43429448….
(E and D being the name of the column in Briggs’ calculation – see above).
There I probably must distinguish between what he wrote and what can be deduced from what he wrote.
In the Chapter 6, he computed –as we have seen in an example (he could have taken any other) the log of number X=1.0000 00000 00000 01 and he found –of course – 0.00000 00000 00000 04342 94481 … etc
We can infer therefore he was conscious of the role of the constant 0.43429448… in the “golden rule”.
But he was probably not aware of the extent of his discovery:
0.43429 = 1/ln(10) =
log(e), and ln(1+t) = t
Briggs and HP35 side by side.
1) To calculate the
logarithm of a number t, Briggs’ idea was to to bring this number close to 1
by taking repeated square roots (m times).
When a number of the form 1.00000 00000 0000 xxxxx, very close to 1, is reached
(1+x in which x is very small) he discovered his “golden rule”:
log(1 +x) = k x
or
ln(1 + x) = x.
To get back to log
(t) or ln (t), he just needed to multiply by
![]() .
.
Let's take –for
example- the case of t=10 and let's calculate ln(10), taking 54 square roots:
Briggs did
![]() =
=
![]()
and with the
« golden rule » he subtracted 1:
![]() =
=
![]() .
.
The final result is there, doubling and doubling the previous result 54 times …
![]() =
=
![]()
(In fact Briggs knew only base 10 logarithms, but that fact doesn't change the rationale).
This is the main Briggs discovery (by continued mean numbers - 'Numeri continue Medii').
But his 'Arithmetica Logarithmica' is a fabulous tool kit that contained a lot of complementary approachs.
In fact, in a practical way, Briggs described several methods to build his
logarithms tables (Continued means - square roots-, use of prime numbers, use
of finite differences, subtabulation and interpolation, and the 'radix
method' (see below historical appendix).
With his methods, Briggs produced a table of the logarithms of integers from 1 to 20000 (Chiliads = kilos) and from 90001 to 100 000, with 14 decimal places.
This table has been recently (2010) completed and corrected with the help of computers (D. Roegel, project LORIA).
The 'radix method'
is introduced in the Chapter 14 of Arithmetica that shows how to use these tables to
find the logarithm of a number and vice-versa (or Chapter. 12 of the Vlacq's
edition ; Briggs's Ch 12 & 13 being omitted).
It is the procedure used in the HP-35.
To find Log(N), N is divided successively by N° (which is the largest tabulated value found in the tables of the Chiliads), next by
N°(1+q1), then by N°(1+q1)(1+q2) etc until N or the desired accuracy is reached.
(The qi are decimal fraction part found during the process ; the division being
made by successive subtractions).
At the end of the process: N <>
N°(1+q1)(1+q2)...(1+qn).
Note that the logarithms of the factors are found from the table (Chiliades or radix tables).
In his example, Briggs used the Chiliads table and a table of radix (numbers of the form ![]() with
their logarithms : 1.0002, 1.00007 etc).
with
their logarithms : 1.0002, 1.00007 etc).

Log(2966.82051456) is searched.
Divisor 2966 is subtracted first, giving 0.82051456. Its decimal log is found in the Chiliads.
From this number only 2 times 0.2966 = 0.5932 can be subtracted giving 0.22731456 for result (right column).
The first quotient is 1.0002.
The value 0.5932 is reported in the left column and added to 2966 giving : 2966.5932
This is the first step ; the decimal
log of the first quotient 1.0002 is found in the radix table.
The spreadsheet below shows the 11 steps for 14 decimal place precision.
| 2966,000000 | 2966,820514560000 | ||||||
| 2966,000000000000 | - | ||||||
| 0,820514560000 | |||||||
| A | 0,593200000 | + | 0,593200000000 | - | 0,296600000000 | 2 | 1,0002000000000 |
| 2966,593200000 | 0,227314560000 | ||||||
| B | 0,207661524 | + | 0,207661524000 | - | 0,029665932000 | 7 | 1,0000700000000 |
| 2966,800861524 | 0,019653036000 | ||||||
| C | 0,017800805 | + | 0,017800805169 | - | 0,002966800862 | 6 | 1,0000060000000 |
| 2966,818662329 | 0,001852230831 | ||||||
| D | 0,001780091197 | + | 0,001780091197 | - | 0,000296681866 | 6 | 1,0000006000000 |
| 2966,820442420370 | 0,000072139633 | ||||||
| E | 0,000059336409 | + | 0,000059336409 | - | 0,000029668204 | 2 | 1,0000000200000 |
| 2966,820501756770 | 0,000012803225 | ||||||
| F | 0,000011867282 | + | 0,000011867282 | - | 0,000002966821 | 4 | 1,0000000040000 |
| 2966,820513624060 | 0,000000935943 | ||||||
| G | 0,000000890046 | + | 0,000000890046 | - | 0,000000296682 | 3 | 1,0000000003000 |
| 2966,820514514100 | 0,000000045896 | ||||||
| H | 0,000000029668 | + | 0,000000029668 | - | 0,000000029668 | 1 | 1,0000000000100 |
| 2966,820514543770 | 0,000000016228 | ||||||
| I | 0,000000014834 | + | 0,000000014834 | - | 0,000000002967 | 5 | 1,0000000000050 |
| 2966,820514558610 | 0,000000001394 | ||||||
| K | 0,000000001187 | + | 0,000000001187 | - | 0,000000000297 | 4 | 1,0000000000004 |
| 2966,820514559790 | 0,000000000207 | ||||||
| L | 0,000000000208 | + | 0,000000000208 | - | 0,000000000030 | 7 | 1,0000000000001 |
| 2966,820514560000 | 0,000000000000 |
Basically it is an addition,
subtraction and shift process applied, in this example, to X = 2966.82051456
At each step of the process (say B) the number found previous step (2966.5932)
left column is shifted right accordingly (105
* 0.029665932) column 3 and subtracted repeatedly until overdraft to the number
in right column (0.22731456 - 7 * 0.029665932 = 0.207661524). The same number
0.207661524 is added to number in left colum.
The right column tends to 0 while the left approaches 2966,82051456.
The fractional part of X is resolved in factors 1.xx...xxr where r is a digit
{1,2 ...8,9} : In the example 2966 * 1,0002 * 1,00007 * 1,000006 etc
Note that the straight division gives 2966.82051456 / 2966 = 1.00027664
This latter result can serve as a guide to find the quotients in the process
: Briggs noted this result in the fist line of his calculation ; see above
2966820514 (100027664.
Step 1 : 2966.82051456 / 2966 = 1.00027664
Step 2 : 1.00027664 / 1.0002 = 1.000076625
Step 3 : 1.0000766625 / 1.00007 = 1.000006625
etc
See the English translation of CH. 14 on the Ian Bruce site.
The final result is found adding the logarithms together (end of page 28) : 'Logarithmi', etc.
2) In the J.E Meggit's algorithm, the following product is formed
![]()
and we bring it
very close to 1, by selecting parameters
![]() properly,
properly,
![]()
We remember Briggs and write very close to 1,
![]()
Having the constants
![]() stored
in ROM, the final result is simply:
stored
in ROM, the final result is simply:
![]() .
.
It can be easily
shown that the algorithm leading to the quotient
![]() is
very close to the division process: y is divided by x using repeated
subtractions.
is
very close to the division process: y is divided by x using repeated
subtractions.
It only differs from a normal division in that the divisor (“pseudo divisor”) is
being constantly updated by addition of
![]() instead
of being constant (JE Meggitt, p 213, J. Laporte [7] & [8]).
instead
of being constant (JE Meggitt, p 213, J. Laporte [7] & [8]).
The Meggitt's variant of the Briggs radix method used radices
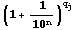 (numbers
2, 1.1, 1.01, 1.001 etc) instead of
(numbers
2, 1.1, 1.01, 1.001 etc) instead of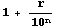 (numbers
like 1.00r or 1.000r) but each one can be repeated up to 9 times
(cf. exponents qj). In both
approaches, the base in which the logarithm is evaliuated is determined by the
base of the stored constants, on paper or in silicon memory.
(numbers
like 1.00r or 1.000r) but each one can be repeated up to 9 times
(cf. exponents qj). In both
approaches, the base in which the logarithm is evaliuated is determined by the
base of the stored constants, on paper or in silicon memory.
When Meggitt wrote in his paper : "the method used is essentially Briggs method" (op. cit. p.211), he referred to the radix method.
J. LAPORTE
2005,
2006, 2012, 2014.
[1]
Henry Briggs.
Arithmetica
Logarithmica.
London 1624.
[2] J.
E. Meggitt,
Pseudo Division and Pseudo Multiplication Processes, IBM JOURNAL APRIL
1962
[3] A. Ralston and H. S. Wilf, Mathematical Methods for Digital Computers, John
Wiley and Sons, Inc., 1960.
[4] J. H. Wensley, “A Class of Non-Analytical Iterative Processes,” The Computer
Journal, 1, No. 4, 163 (Jan. 1959).
[5] Erik Vestergaard. En revolution i regnekunsten, Forlaget ABACUS, Denmark,
1996.
[6] Herman Goldstine.
A
History of Numerical Analysis from the 16th through the 19th Century.
Springerverlag, 1977.
[7] Jacques Laporte,
HP 35 Logarithm Algorithm,
(a step by step comment of the HP35 Rom code), December 2005,
[8] Jacques Laporte,
Digit by digit Methods
June 2006.
[9] Denis Roegel, A reconstruction of the tables of Briggs' Arithmetica Logarithmica, Jan 2011.
THE RADIX METHOD : AN HISTORICAL APPENDIX.
The « radix method » has been rediscovered at different epochs, by different authors ( T. Weddle, R. Flower, P. Gray …), in different forms.
Basically, it’s a reversible procedure
that leads (using the definition of logarithms
![]() and
and
![]() )
to a number close to 1 where the golden rule can be applied ; the return process
yielding the final result.
)
to a number close to 1 where the golden rule can be applied ; the return process
yielding the final result.
According to Florian
Cajori (A History of Mathematics, 1893, p 155) “A famous method of computing
logarithms is the so-called "radix method". It requires the aid of a table of
radices or numbers of the form
![]() with
their logarithms. The logarithm of a number is found resolving the number into
factors of the form
with
their logarithms. The logarithm of a number is found resolving the number into
factors of the form
![]() and
adding the logarithms of the factors.
and
adding the logarithms of the factors.
Strictly speaking, in a radix table, in
![]() ,
the number "r" (as named by Cajori) is an integer less the 10.
,
the number "r" (as named by Cajori) is an integer less the 10.
A modern radix table can be found in the "Handbook of Mathematical functions" by
Abramowitz and Stegun, p.114 -115.
The earliest appearance of this method is in an anonymous "Appendix" (very probably due to Oughtred) to Edward Wrights’s 1618 edition of Napier’s Descriptio.
It is fully developed by Briggs who, in his Arithmetica logarithmica, 1624 Ch 24, that gives a table of radices.
The radix method as exposed by Briggs uses the following main equation derived from the logarithm definition :
(1)
![]()
(2)![]()
Briggs factorized the second part of expression 2 :
![]()
For example :
7.854 being taken as (x + y) ( 7 + 0.854) :
7.854 = 7 * 1.122 = 7 * 1.1 * 1.02
J.E. Meggitt was a IBM's researcher. He has automated the Briggs' method and had reduced the number of values (radices logarithms) stored in ROM : in fact to 7 (compared to 99 in the paper table Briggs).
Hence the second part of expression 2 is factorized by
![]()
which is sometimes longer.
For example in the case of 7.854, the result found is
7.854 = 7 * 1.1 * 1.01 * (1.001)9 * (1.0001)8 ...
Each factor can be taken up to 9 times.
HOW TO BUILD A RADIX TABLE : The Robert Flower's presentation.
The method presented by Briggs in the Chapter 6 of Arithmetica Logarithmica is based on a sequence of continued mean numbers formed by the evaluation of successive square roots of 10.
This table of successive square roots of 10 can be regarded as a 'radix table' and used to find logarithms from numbers and numbers from logarithms.
In
his book
"The Radix, a new way of making logarithms" (1771), Robert Flower
introduced an "instrument or rule, calculated for that purpose, called the Radix
consisting of one hundred numbers and their logarithms" : the number 10 + 99
numbers of the form
![]() .
.
This table was "constructed to 23 places, by two others constructed for that purpose (p.61) :"
-
the square-square radix made by extracting the square roots of ten to 22 or 23
places,
- the cube-square radix made by extracting Cube Roots of ten to 23 places.
Here is an example of use of the Cube Root Radix, To find the log of 2 :
(op. cit p 6, the Cube Root Table, on the Google Books digital copy)

& p.7 the evaluation of log(2) using the log found in the table.

Flower approximates the number 2, by finding in the Radix table, "the nearest root of ten to the given number 2" : 2.1544346900. He puts down the Log found in the table in the right column.
He approximates 2 in the left column, by multiplication or division and evaluates the log, in the right column, by addition or subtraction (definition of the logarithms). It "happens that the Numbers are approximated somewat sooner by the Square than by the Cube, but these two may be used together as one Radix, and then the intervals will be much less, and coasequently the approximation thereby greatly accelerated" (op cit p.9).

Finally here is a Maxima program to print the cube or square root radix table.
fpprec:70$
set_display(ascii)$
/* Square Radix of 10, k=2*/
/* Cube Radix of 10, k=3*/
x:
10$
k: 2$
foo(x,i) := block(j: k^i, x: x^(1/(j)), bfloat(x))$
s: openw("/Users/jacqueslaporte/Documents/radix_table.dat")$
for i : 1 thru 35 do block(printf (s, "~D: ~5t~h ~80t~f~%", i, foo(10,i) ,
float(1/(k^i)) ) )$
close(s)$
printfile("/Users/jacqueslaporte/Documents/radix_table.dat")$