DIGIT BY DIGIT Methods
The purpose of this
paper is to present the “pseudo division” algorithm and to show how – at the
price of a slight modification of the divisor (referred as “pseudo divisor”) –
this method can compute different functions as logarithms or arc tangents.
This approach is a generalization by J.E. MEGGITT (1962) of an ancient method invented by Henry BRIGGS (circa 1624) to elaborate his logarithm tables.
Known as “digit-by-digit” methods, this class of algorithms is fast and requires only basic operators: adders and shifters.
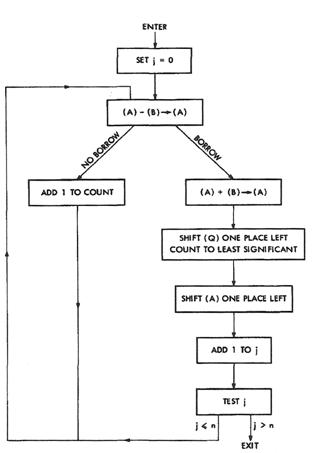
The following chart is extracted from the Meggitt’s paper p.211.
It represents the flow diagram for an elementary divider and it is exactly the core divider implemented in the HP 35’s ROM (the only difference is that register Q is filled in the opposite order in the HP 35 case, from right to left).
The division is
conducted by a rather simple process of repeated subtractions (y/x).
Register A contains the number y and register B the number x. Each register is
correctly dimensioned and the numbers are aligned as needed.
The number of
subtractions is recorded in register Q, which is a counter.
 A
small numeric example will make it clear.
A
small numeric example will make it clear.
We calculate 17/5 (y=17, x=5) by repeated subtractions and we note the
calculations as JE Meggitt did p. 214 for logarithms.
The result y/x = 3.4
is just the “decimal expansion” of the quotients digits:
![]()
![]()
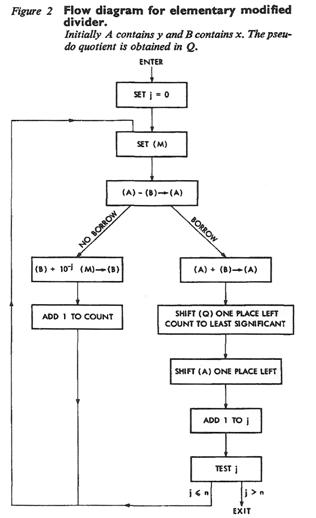
In the second chart
(same page 211), is represented a the flow diagram of a “modified” divider.
After each subtraction the “pseudo” divider, register B on the diagram, is
updated.
The content of the modifier register M, shifted j places to the right, is added
to the divisor:
(B) + 10-j (M) -> (B).
The quotient formed
in the Q register – the
![]() digits-
is named “pseudo” quotient.
digits-
is named “pseudo” quotient.
Changing the modifier can lead to various routines like, log, arc tan, etc.
1) Computing logarithms with pseudo operations.
In the case of the
pseudo divider represented below, the digits
![]() (we
already met in the logarithm article) have been calculated to make the following
expression as small as possible:
(we
already met in the logarithm article) have been calculated to make the following
expression as small as possible:
![]()
This operation
(pseudo division) only differs from a genuine division in that the pseudo
divisor is constantly updated by addition of
![]() (instead
of being constant) (eq 5 Meggitt p. 213).
(instead
of being constant) (eq 5 Meggitt p. 213).
To each pseudo-divider is associated a pseudo-multiplier.
In this case the pseudo-multiplier will calculate
![]() .
.
These digit-by-digit
methods are quite general and it must be understood that the Cordic can be seen
as a particular case were the Briggs’s method is applied to complex logarithm
(e.g. in arc tan calculation, the pseudo quotients
![]() are
calculated to make the imaginary part of the expression
are
calculated to make the imaginary part of the expression
![]() as
small as possible but positive).
as
small as possible but positive).
Let’s elaborate a little bit.
Page 214 of his article, J.E. Meggitt took the example of the pseudo division of y=67719 and x=21608.
Normal division gives: y/x = 3.13397816, but “pseudo division” gives log(1+(y/x)).
The calculation
scheme is -as explained above- slightly different, the “pseudo” divider, x in
register B, is updated, after each subtraction; that gives (to write shorter I
use
![]() in
the expression
in
the expression![]() ):
):
|
j |
B |
A |
Count |
Q |
x' |
y' |
M |
x M |
(x + y) / x M |
|
|
|||||||||
|
0 |
21608 |
67719 |
21608 |
67719 |
|||||
|
|
21608 |
-21608 |
|||||||
|
|
43216 |
46111 |
1 |
43216 |
46111 |
2 |
|||
|
|
43216 |
-43216 |
|||||||
|
|
86432 |
2895 |
2 |
2 |
86432 |
2895 |
4 |
86432 |
1.03349453905961 |
|
|
KO |
||||||||
|
|
|||||||||
|
1 |
86432 |
2895 |
0 |
20 |
|||||
|
|
KO |
||||||||
|
|
|||||||||
|
|
|||||||||
|
2 |
86432 |
2895 |
|||||||
|
|
864.32 |
-864.32 |
|||||||
|
|
87296.32 |
2030.68 |
1 |
87296.32 |
2030.68 |
4.04 |
87296.32 |
1.02326191986100 |
|
|
|
872.9632 |
-872.9632 |
|||||||
|
|
88169.2832 |
1157.7168 |
2 |
88169.2832 |
1157.7168 |
4.0804 |
88169.2832 |
1.01313061372376 |
|
|
|
881.692832 |
-881.692832 |
|||||||
|
|
89050.976 |
276.023968 |
3 |
203 |
89050.97603 |
276.023968 |
4.121204 |
89050.97603 |
1.00309961754828 |
|
|
KO |
||||||||
|
|
|||||||||
|
|
|||||||||
|
3 |
89050.976 |
276.023968 |
|||||||
|
|
89.050976 |
-89.050976 |
|||||||
| 89140.027 | 186.972992 | 1 | 89140.02701 | 186.972992 | 4.125325204 | 89140.02701 | 1.00209752002825 | ||
| 89.140027 | -89.140027 | ||||||||
| 89229.167 | 97.832965 | 2 | 89140.02701 | 97.83296496 | 4.1294505292040 | 89229.16704 | 1.00109642360464 | ||
| 89.229167 | -89.229167 | ||||||||
| 89318.3962 | 8.603797925 | 3 | 2033 | 89229.16704 | 8.603797925 | 4.1335799797332 | 89318.3962 | 1.00009632727737 | |
| KO |
At the end of each of the 3 possible pseudo-divisions (j=0, 2, 3), the values of
![]() are:
are:
2895, 276.023968, and 8.603797925.
Note that minimizing y’ (small as possible but y’ > 0) is equivalent to drive
the ratio
![]() close
to 1; we will see below that this latter is the most interesting to consider for accuracy.
close
to 1; we will see below that this latter is the most interesting to consider for accuracy.
After the pseudo divisions: y’ = 8.60379792 and the pseudo quotients are “2033”,
so we can form the expression:
![]()
which is already a very good approximation of ln(1 + y/x) = ln (1 + 3.1339781562) = ln(4.1339781562).
In the previous calculation, by making
![]() as
small as possible
as
small as possible
![]() we
have co transformed x and y, and we have - to the limit- y’ = 0, and therefore
we
have co transformed x and y, and we have - to the limit- y’ = 0, and therefore
![]() and
and
![]() .
.
Now, we have to take into account the small difference:
![]()
that is to say :
![]()
![]()
and the result we search is:
![]()
working on
![]() with
with
![]()
it comes:
![]()
In our example:
![]() and
and
![]()
Here we met again the Briggs’
proportionality golden rule (![]() when
t very small ; in modern language
when
t very small ; in modern language
![]() ):
):
![]()
So we add 0.00009632727737 to our previous result , and we have the final result:
ln (1 + 3.1339781562) = 1. 4192403759
It is word for word the definition of the
Brigg’s radix method as a reversible procedure that leads (using the definition
of logarithms
![]() and
and
![]() )
to a number close to 1 where the golden rule can be applied ; the return process
yields the final result.
)
to a number close to 1 where the golden rule can be applied ; the return process
yields the final result.
The only difference is that here the result is found
resolving the number into factors of the form
![]() and
adding the logarithms of the factors.
and
adding the logarithms of the factors.
The Meggitt’s approach is quite general and can be applied to evaluate log z
(instead of log(1 + y/x) by simply taking y = 1 –z, but the original
presentation shows the proximity with the straight division algorithm and the
Briggs’ approach.
I will now show how to derive the former expression from the pseudo-expression recurrence expressions.
We write simply the pseudo division scheme:
![]()
(in the normal division x is constant).
If we bring up (2) in (1), we have:
![]()
![]() (for
a j).
(for
a j).
For k factors, we have (all the recurrences for a j) :
![]()
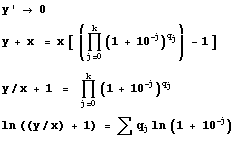
In practice however, we will make a fixed number of pseudo-divisions (5 in the HP calculators implementation) and expression (3) is never null so we have to take care of the remainder. See the refinements of the actual implementation in the HP 35 ROM.
2) Computing “arc tan x” with pseudo
operations.
The same scheme is applied by J.E.
MEGGITT to the case of the inverse trigonometric functions and it seems
difficult to understand –for many of my readers- that it is exactly the same
algorithm, named CORDIC by J. VOLDER.
The common denominator of these algorithms could be named “digit-by-digit”
methods and they date back to Briggs, 3 centuries ago and were studied by many
authors (e.g. the divide algorithm of the IBM/360 Model 91 that cotransforms
y/x, until the divisor is close to 1 (3) ).
One difficulty is that Meggitt’s does not follow the trigonometric classical presentation for the successive rotation formulas, but uses the complex numbers notation.
This extension to the complex domain is just another paradigm.
I will use very elementary mathematics.
The linear transformation that carries a vector x into another u obtained by
rotating through an angle
![]() is
called a rotation.
is
called a rotation.
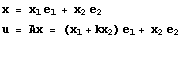
We can choose another paradigm and
consider a rotation as the multiplication of 2 complex numbers. As a matter of
fact the complex number z has 2 forms of representation
![]() and
and
![]() (rectangular
and polar) and the product of 2 complex numbers z1 and z2:
(rectangular
and polar) and the product of 2 complex numbers z1 and z2:
![]()
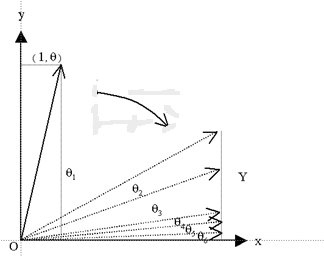
For the inverse trigonometric function,
the process starts from a point in the plane
![]() representing
the complex number :
representing
the complex number :
![]() or,
or,
![]()
by definition
![]() and
and
![]()
Now we rotate the vector “clock wise” to
the x axis, minimizing thus the Y component and counting the number of rotations
(![]() )
for each small angle
)
for each small angle
![]() .
.
We start the series of rotations by the angle
![]() .
.
This rotation clock wise writes:
![]() (the
negative sign expressing the clock wise rotation and the angle is
(the
negative sign expressing the clock wise rotation and the angle is
![]() .
.
Now we can see how the Cordic rotations transform in digit-by-digit recurrence
expression (as written by Meggitt).
We write the first rotation:
![]()
then we expand :
![]()
Finally we have the recurrence formulas:
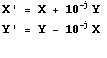
These formulas are very close to the logarithm recurrences established above, but the pseudo divisor is different:
![]()
3) Briggs, Meggitt, Volder, and others.
The Cordic algorithm (Volder 1956) is
nothing but a trigonometric application of the “digit-by-digit” methods known by
Briggs and others three centuries ago.
Meggitt applied (1962) the pseudo division and pseudo multiplication methods to
a number of functions.
A lot of authors are re-discovering –from time to time- this approach, bringing
enhancements (speed and/or accuracy).
There is nothing magical in this
parentage: the basic root scheme is an iterative cotransformation of a pair of
numbers (x,y) leaving a bivariate function F(x,y) invariant (cf. 7).
You’ll find below ancient tracks to follow.
Jacques Laporte
Friday, 09 June 2006
(1) J.E. MEGGIT, Pseudo Division and Pseudo Multiplication processes, IBM
Journal, Res & Dev, April 1962, 210-226.
(2) J .E. VOLDER, “The Cordic Trigonometric Computing Technique”, IEEE
Transactions on Electronic Computers, Sept. 1959.
(3) S. F. ANDERSON, J. G. Earle. R. E. Goldschmidt, and D. M. Powers,
"The IBM System/360 Model 91: Floating-point Execution Unit," IBM J . Res.
Develop. 11, 34-53 (1967).
(4) Vladimir BAYKOV - Vladimir SMOLOV: "Hardware implementation of the
elementary functions in computers" (in Russian), 1975, Leningrad State
University, a few pages published here:
http://baykov.de/cordic1972.htm ,
(5) H. E. SALZER, "Radix Tables for Finding the Logarithm of Any Number
of 25 Decimal Places," in Tables of Functions and of Zeros Functions, National
Bureau of Standards Applied Mathematics Series n° 37, 1957.
(6) J. S. WALTHER, "A Unified Algorithm for Elementary Functions," Proc.
AFIPS 1971 Spring Joint Computer Conference, pp. 379-385.
(7) TIEN CHI CHEN, Automatic Computation of Exponentials, Logarithms,
Ratios and Square Roots, IBM J. RES. DEVELOP. July 1972.
Note on the “radix method”.
The “radix method” is defined by Florian Cajori (A History of Mathematics, 1893,
p 155) as “A famous method of computing logarithms is the so-called "radix
method". It requires the aid of a table of radices or numbers of the form
![]() with
their logarithms.
with
their logarithms.
The logarithm of a number is found resolving the number into factors of the form
![]() and
adding the logarithms of the factors.
and
adding the logarithms of the factors.
The earliest appearance of this method is in an anonymous "Appendix" (very probably due to Oughtred) to Edward Wrights’s 1618 edition of Napier’s Descriptio.
It is fully developed by Briggs in his 1624 Arithmetica logarithmica (Ch. 14 or Ch. 12 of the Vlacq's edition - available on Google Books).
The procedure followed by Meggitt is in fact the Briggs' method.
There is no hole between Briggs (1624) and Meggitt (1962), and for example,
Robert Flower gives in 1771 (“The radix a new way of making Logarithms”, London)
a description very similar.
Jacques LAPORTE
13/11/2006, revisited Feb 2012
|
|
fig 1 : “Arithmetica Logarithmica” Chapter 14 Radix table

fig2 : same chapter, example of calculation using a Radix table