|
The two scales on the back of the slide marked S and T are the
sine and tangent scales respectively.
|
|
|
|
Sines
|
|
|
 The S
scale is divided to read in degrees and minutes from about
0°34′ to 90°. It is designed to be used with the
A and B scales.
|
|
|
|
Example:
Find the sine of 21°.
|
|
|
|
Set the
slide to bring 21 on the S scale under the right-hand fixed
hairline on the back of the rule. Example shown in Figure 20a.
Turn the rule over, and read
358 on the B scale under the right index of the A scale.
Example shown in Figure 20b.Note that the values of sines found
on the right-hand half of the A and B scales range from 0.1 to
1.0 and those on the left-hand half range from 0.01 to 0.1.
Therefore, our answer in this example is 0.358.
|
|
|
|
When
given the sine, the procedure is reversed to find the angle.
|
|
|
|
Example:
Find the angle whose sine is 0.126.
|
|
|
|
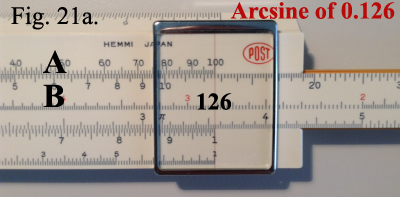
Since the
sine is greater than 0.1, 0.126 is located on the right-hand
segment of the B scale. Draw the slide to bring 126 on the
right half of the A scale. Example shown in Figure 21a.
Turn the rule over, and read the angle
7°15′ on the S scale under the fixed hairline.
Example shown in Figure 21b.
|
|
|
|
Alternate Method (Sines)
|
|
|
|
Remove the
slide from the rule and re-insert so that the S, L en T scales
are face up. With the slide centered so that the indices of the
A scale line up with the ends of the S scale, sines can be read
on the A scale directly opposite any angle on the S scale. Thus,
to find the value of sin 7°, set the cursor hairline over 7 on
the S scale and read the answer 0.122 under the hairline on the
A scale. Example shown in Figure 22.
|
|
|
|
Tangents
|
|
|
|
The T scale is divided in degrees
and minutes from about 5°45′ to 45°. It is designed to be used with the
C and D scales.
|
|
|
|
Example: Find the value of tan 35°.
|
|
|
|
Set 35 on the T scale under the
right-hand fixed hairline on the back of the rule. Example shown in Figure 23a.
Turn the rule over and read the answer 0.7000 on the C scale over the right index of the D scale.
Example shown in Figure 23b.
Note that the values of tangents
of angles from 5°45′ to 45° range from 0.1 to 1.0.
|
|
|
|
Alternate Method (Tangents)
|
|
|
|
Turn the slide rule over as
described in the alternate method for using the S scale and read directly from the
T scale to the D scale or vice versa.
Thus, to find the value of tan 35°, set the cursor hairline over 35 on the T scale
and read the answer 0.007 under the hairline on the D scale. Example shown in Figure 24.
|
|
|
|
Tangents of Angles from 0°34′ to 5°45′
|
|
|
|
The values of tangents and sines of
angels smaller than 5°45′ are so nearly alike that they may be considered identical
for slide rule computations. Consequently, for angles from 0°34′ to 5°45′,
tangents can be read directly using the S scale and the left half of the A or B scales,
as described in the section of sines.
|
|
|
|
Tangents of Angles greater than 45°
|
|
|
|
Using the relationship
|
|
|
|
|
|
|
|
tangents for angles greater than 45° can be directly computed on the slide rule.
|
|
|
|
Example: Find tan 69°.
|
|
|
|
Solution: 90 – 69 = 21.
Set 21 on the T scale under the right-hand fixed hairline. Example shown in Figure 25a.
The answer, which is the reciprocal of tan 21, is read directly on the D scale under the
left index of the C scale as 2.605. Example shown in Figure 25b.
Note that for angles between 45° and approximately 84° the value of the tangent
ranges from 1 to 10.
|
|
|
|
When in the above relationship 90 – x
is less than 5°45′, the left half of the S scale is used in making the computation.
As pointed out above, the sines and tangents of small angles may be considered equal for slide
rule purposes.
|
|
|
|
Example: Find tan 88°.
|
|
|
|
Set 2 on the S scale (90 – 88) under
the right-hand fixed hairline. Example shown in Figure 26a.
Turn the slide rule over and read the answer 28.6 on the A scale over the left index of the B
scale. Example shown in Figure 26b.
Using this method, tangents of angles up to 89°25′ can be read directly.
|
|
|
|
Sines and Tangents of Very Small Angles
|
|
|
|
For determining the sine or tangent
of a very small angle, two gauge points are provided on the S scale. The one identified by
the symbol (′) is called the minutes gauge point and is fount next to the 2° mark
on the S scale. The second gauge point marked (″) is found near the 1°10′
mark on the S scale. Example shown in Figure 27. They represent the value of the angle in
radians. Their use is based on the fact that for very small angles, sin x = tan x = x
(in radians), approximately.
|
|
|
|
Example: Find sin 3′.
|
|
|
|
Since sin 3′ = 3′ (in radians),
solve 3 × 1′ (in radians). The procedure when using these gauge points is the same
as the use of the CI and D scale combination for multiplication. With the slide rule turned
so that the trig scales are face up, set the minutes gauge mark under the 3 on the A scale.
Over the right index on the S scale, read 0.000873 on the A scale. Example shown in Figure 28.
|
|
|
|
Example: Find sin 3″.
|
|
|
|
Set the second gauge mark under 3
on the A scale. Over the left index on the S scale, read 0.0000145 on the A scale.
Example shown in Figure 29.
|
|
|
|
The decimal point in the above
examples is located by noting that:
|
|
|
|
1′ – 0.0003 radians (approximately)
|
|
1″ – 0.000005 radians (approximately)
|
|
