DIVISION
The slide rule procedure for division is just the reverse of multiplication. For example to solve (see Figure 7):
  6  = 2
 
3
Set 3 on the C scale over 6 on the D scale. Under the left index of the C scale read the answer 2 on the D scale.
 
If the slide extends to the left, as for example when dividing:
  12  
 
2
as shown in Figure 8, then read the answer 6 on the D scale under the right-hand index of the C scale.
OTHER METHODS TO MULTIPLY AND DIVIDE
The A and B scales, which are idential in scale arrangement, are similar in construction to the C and D scales, except that they are half size. This makes it possible to place two segments end to end in the same length occupied by the C and D scales. For convienence in use, the right-hand half of the A and B scales is numbered from 10 to 100, since this section is actually a continuation of the left half (on Post’s pocket size rules, the zeros are omitted because of lack of space).
In Figure 9, the setting of the slide rule illustrates the solution to the problem 4 × 9 = 36 solved on the A and B scales. The left index of B is set under the 4 on the A scale. Over 9 on the B scale we read the answer 36 on the A scale.
 
Dividing with A and B scales
For division we follow the reverse procedure. Example shown in Figure 10:
  36  = 4
 
9
Set 9 on the B scale under 36 on the A scale. Over the left index on the B scale, read the anwer 4 on the A scale.
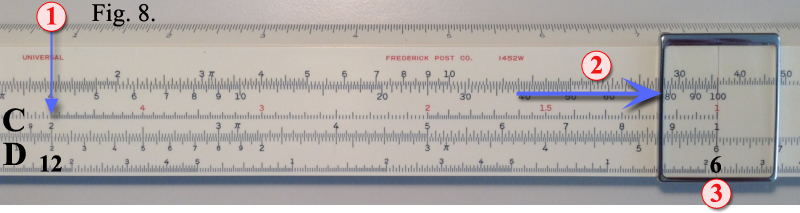
Use of CI Scale
Multiplication problems can be solved very efficiently using the CI scale in conjunction with the D scale. The CI scale is exactly the same as the C scale except that it has been turned end for end, and consequently reads from right to left.
To multiply using the CI and D combination of scales, refer to the setting in Figure 9 for the solution of the problem 6 × 3.33 = 20.
With the cursor hairline set over 6 on the D scale, draw the slide to bring 3.33 on the CI scale under the hairline. Under the left index on the CI scale, we find the slide rule answer 2 on the D scale. Example shown in Figure 11.
To locate the decimal point, we take as round figures 6 × 3 = 18. Our answer, therefore, is 20.
 
Multiplying More Than Two Factors
The CI–C–D scale combination is particularly useful in solving multiplication problems involving more than two factors. For example: Find the volume of a wall 15.5 feet long by 8 feet high by 0.55 feet thick.
Solution: Set the cursor hairline over 8 on the D scale. Set the slide to bring 155 on the CI scale under the hairline. Example shown in Figure 12a. Now set the hairline over 55 on the C scale. Read 682 under the hairline on the D scale. Example shown in Figure 12b.
To locate the decimal point solver mentally: 15 × 8 × .5 = 15 × 4 = 60. The correct answer, therefore, is 68.2 cubic feet.
Notice that in the above example only one setting of the slide is necessary to solve two multiplications simultaneously. The partial answer 124, from 8 × 15.5 is on the D scale under the left index on the C scale. Since the second step in the problem is to multiply by 0.55, it is necessary only to set the hairline to 55 on the C scale and read the answer, 68.2, on the D scale without any regard to the partial answer.
– 6 –