|
The Scales.
|
 On the
face of the slide rule you see four scales A, B,
C and D and on the back face of the slide, you
see three scales S, L and T. Of these
scales A, B, C and D are for
multiplication, division, squaring, extraction of a square root,
cubing and extraction of a cube root, T and S are
for trigonometrical functions, a sine and a tangent respectively,
and L for logarithms. Naturally on the slide rules for
beginners the scales on the back face, S, L and
T are often destroyed.
|
|
The
greatest importance in using a slide rule is the reading. The
accuracy in reading means the accuracy in calculation. Hence
the practice of a slide rule is the practice of its reading.
|
|
Of these
scales A and B are exactly the same and so are
C and D. To begin with A and B, you
will read 1 at the left end of the scale, and then gradually 2,
3, 4......to the right. At the center, you read 10; then to the
right you will read 20, 30, 40......until you come to 100 at the
right end.
|
|
|
|
The sub-divisions represent each, either
1/10 or
1/5 or
1/2 of
the sub-division just like those on any rule of the decimal
system.
The only trouble for beginners would be the un-equality
or variations of divisions; but they will overcome it after a
little practice.
|
|
Repeating
the explanation, read first the large division, then the sub-division
and then the lesser sub-division; these three figures put together
in order represent the digit value of the point on the scale. A point
between lines, or a point that is not marked, is to be read by
inspection.
|
|
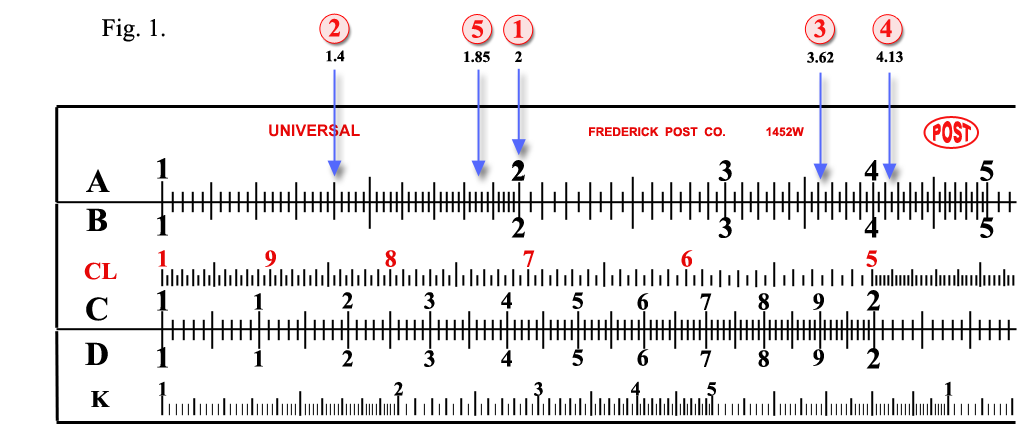
For
examples five points, (1), (2), (3)......, (5) are taken on
A, B and four points, (1), (2)......, (4) are taken
on C, D scales (see, Fig. 1):
(1) on A, B, is to read “2,” (2)
“1.4,” (3) “3.62,” (4)
“4.13,” (5) “1.85”. Furthermore
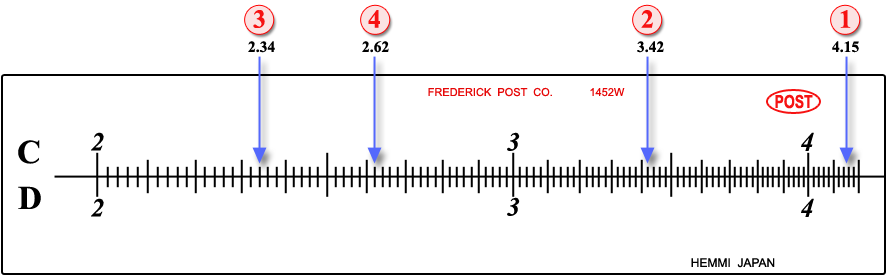
(1), (2), (3), (4)......on C, D represent
4.15, 3.42, 2.34, 2.62,......respectively.
|
|
Note
the divisions on C and D scales of a 5″ slide rule
are exactly the same as those on the left half section of A
and B of a 10″ slide rule.
|
|
