|
Square and Square roots
|
|
|
 Note that the relationship between
A and the D scales is such that for numbers appearing on the D scale the squares can be
found directly above on the A scale. Conversely, the square roots of numbers appearing
on the A scale are directly below on the D scale. Note that the relationship between
A and the D scales is such that for numbers appearing on the D scale the squares can be
found directly above on the A scale. Conversely, the square roots of numbers appearing
on the A scale are directly below on the D scale.
|
|
|
 Thus, to find the square of any
number, set the hairline over that number on the D scale. The square will be found under
the hairline on the A scale. Example
shown in Figure 13. Thus, to find the square of any
number, set the hairline over that number on the D scale. The square will be found under
the hairline on the A scale. Example
shown in Figure 13.
|
|
|
-
Set the hairline over 5 on the D scale,
the square 25 is found under the hairline on the A scale.
-
Set the hairline over 3 on the D scale,
the square 9 is found under the hairline on the A scale.
-
Set the hairline over 2 on the D scale,
the square 4 is found under the hairline on the A scale.
|
|
|
 To find the square root of a number,
the reverse procedure is followed. The hairline is set over the number on the A scale, and
the root is found under the hairline on the D scale. To find the square root of a number,
the reverse procedure is followed. The hairline is set over the number on the A scale, and
the root is found under the hairline on the D scale.
|
|
|
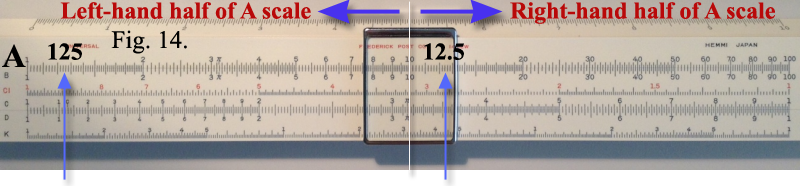
 If the A scale number has an
odd number of digits to the left of the decimal point, it is located on the
left-hand half of the A scale. If it has en even number of digits to
the left of the decimal point, then it is located on the right-hand half of the
A scale. Example shown in Figure 14. Thus, 125 would be found on the left-hand half of the scale and 12.5 would be
found on the right-hand half of the scale. If the A scale number has an
odd number of digits to the left of the decimal point, it is located on the
left-hand half of the A scale. If it has en even number of digits to
the left of the decimal point, then it is located on the right-hand half of the
A scale. Example shown in Figure 14. Thus, 125 would be found on the left-hand half of the scale and 12.5 would be
found on the right-hand half of the scale.
|
|
|
 You can also
make a quick mental calculation to determine if the answer is located
on the left- or right-hand half of the A scale. For example to find
the root of the number of days in a year, 365, the answer is less
then 20. So the answer must be on the left-hand side of the A scale.
Example shown in Figure 15. You can also
make a quick mental calculation to determine if the answer is located
on the left- or right-hand half of the A scale. For example to find
the root of the number of days in a year, 365, the answer is less
then 20. So the answer must be on the left-hand side of the A scale.
Example shown in Figure 15.
|
|
|
|
Cubes and Cube Roots (use of the K scale)
|
|
|
 By using the D scale and K scale
in combination, cubes and cube roots can be found directly on your slide rule (the K
scale does not appear on the POST 4 inch rule). Note that the K scale is made up of three
identical sections placed end to end. Each section is similar in construction to the
D scale except that it is exactly one-third its length. By using the D scale and K scale
in combination, cubes and cube roots can be found directly on your slide rule (the K
scale does not appear on the POST 4 inch rule). Note that the K scale is made up of three
identical sections placed end to end. Each section is similar in construction to the
D scale except that it is exactly one-third its length.
|
|
|
 To find the cube of a number,
set the cursor hairline to that number on the D scale, and read the answer under the
hairline on the K scale. To find the cube of a number,
set the cursor hairline to that number on the D scale, and read the answer under the
hairline on the K scale.
|
|
|
 To find the cube root of a number,
the procedure is reversed, setting the hairline first to the number on the K scale and
reading the cube root under the hairline on the D scale. To find the cube root of a number,
the procedure is reversed, setting the hairline first to the number on the K scale and
reading the cube root under the hairline on the D scale.
|
|
|
|
Locating Numbers on the K scale
|
|
|
 The three segments of the K scale
cover numbers ranging from 1 to 10 for the left-hand section, from 10 to 100 for the
center section and from 100 to 1000 for the right-hand section. See Figure 16. Thus for any number
between 1 and 10 on the D scale, the cube can be read directly off of the K scale
somewhere between 1 and 1000. Conversely, for numbers between 1 and 1000 on the K scale,
the cube roots will be read directly on the D scale somewhere between 1 and 10. For numbers
less than 1 or greater than 10 on the D scale, or less than 1 and greater than 1000 on the
K scale, the decimal point may be moved both before and after the operation to obtain a
number within the range of the scales. In such cases a definite rule may be followed. The three segments of the K scale
cover numbers ranging from 1 to 10 for the left-hand section, from 10 to 100 for the
center section and from 100 to 1000 for the right-hand section. See Figure 16. Thus for any number
between 1 and 10 on the D scale, the cube can be read directly off of the K scale
somewhere between 1 and 1000. Conversely, for numbers between 1 and 1000 on the K scale,
the cube roots will be read directly on the D scale somewhere between 1 and 10. For numbers
less than 1 or greater than 10 on the D scale, or less than 1 and greater than 1000 on the
K scale, the decimal point may be moved both before and after the operation to obtain a
number within the range of the scales. In such cases a definite rule may be followed.
|
|
|
 If the decimal point is moved
n number of places in a value set on D, it must be moved back 3n places in the cube,
which is read on the K scale; or if the decimal point is moved n number of places in a
value set on the K scale, it must be moved back
3/n places in the cube root, which
is read on the D scale. If the decimal point is moved
n number of places in a value set on D, it must be moved back 3n places in the cube,
which is read on the K scale; or if the decimal point is moved n number of places in a
value set on the K scale, it must be moved back
3/n places in the cube root, which
is read on the D scale.
|
|
|
 For example, to find the cube of
0.456, we move the decimal point 1 place to the right. By setting the hairline at 4.56 on
the D scale, we obtain 95 at the hairline on the K scale. According to the above rule, we
now move the decimal point to the left three places and obtain the answer 0.0095.
Example shown in Figure 17a. For example, to find the cube of
0.456, we move the decimal point 1 place to the right. By setting the hairline at 4.56 on
the D scale, we obtain 95 at the hairline on the K scale. According to the above rule, we
now move the decimal point to the left three places and obtain the answer 0.0095.
Example shown in Figure 17a.
|
|
|
 To find the cube of 1214, we move
the decimal point three places to the left. Setting the hairline to 1.214 on D, we find
the cube 1.79 on K. We now move the decimal point back nine places to the right, giving us
the answer 1,790,000,000. Example shown in Figure 17b. To find the cube of 1214, we move
the decimal point three places to the left. Setting the hairline to 1.214 on D, we find
the cube 1.79 on K. We now move the decimal point back nine places to the right, giving us
the answer 1,790,000,000. Example shown in Figure 17b.
|
|
|
 To find the cube root of 0.0052,
the decimal point is moved three places to the right. The hairline is now set over 5.2
on the left hand segment of the K scale. According to the above rule, the decimal point
is now moved back one place to the left, giving the answer 0.173.
Example shown in Figure 17c. To find the cube root of 0.0052,
the decimal point is moved three places to the right. The hairline is now set over 5.2
on the left hand segment of the K scale. According to the above rule, the decimal point
is now moved back one place to the left, giving the answer 0.173.
Example shown in Figure 17c.
|
|
|
|
Reciprocals
|
|
|
 The relationship of the C and CI
scales is such that the reciprocal of any number on either scale can be read for that
number directly opposite on the other scale. For example: The reciprocal of: The relationship of the C and CI
scales is such that the reciprocal of any number on either scale can be read for that
number directly opposite on the other scale. For example: The reciprocal of:
|
|
|
|
|
|
|
 To solve on the slide rule, set
the cursor hairline over 2 on the C scale. Under the hairline on the CI scale, read the
reciprocal 0.5. Example shown in Figure 18a. The position of the decimal point in any reciprocal can be determined by
a mental calculation using round numbers as explained in the section of multiplication.
The procedure may be reversed by setting the hairline to 2 on the CI scale and reading
the reciprocal 0.5 directly below on the C scale. Example shown in Figure 18b. To solve on the slide rule, set
the cursor hairline over 2 on the C scale. Under the hairline on the CI scale, read the
reciprocal 0.5. Example shown in Figure 18a. The position of the decimal point in any reciprocal can be determined by
a mental calculation using round numbers as explained in the section of multiplication.
The procedure may be reversed by setting the hairline to 2 on the CI scale and reading
the reciprocal 0.5 directly below on the C scale. Example shown in Figure 18b.
|
|
|
|
Logarithms
|
|
|
 The L scale on the back of the slide
is a uniformly divided scale which gives the mantissa of logarithms of number read on the
D scale. Example: Find the logarithm of 2. The L scale on the back of the slide
is a uniformly divided scale which gives the mantissa of logarithms of number read on the
D scale. Example: Find the logarithm of 2.
|
|
|
 Set the left index of the C scale over
2 on the D scale. Example shown in Figure 19a. Turn the slide rule over, and read the mantissa 301 on the L scale under
the fixed hairline on the back of the rule. Example shown in Figure 19b. From the principle of logarithms, it is known
that the characteristic for 2 is zero; the logarithm, therefore is 0.301. Set the left index of the C scale over
2 on the D scale. Example shown in Figure 19a. Turn the slide rule over, and read the mantissa 301 on the L scale under
the fixed hairline on the back of the rule. Example shown in Figure 19b. From the principle of logarithms, it is known
that the characteristic for 2 is zero; the logarithm, therefore is 0.301.
|
|