The Radix Method
The radix method is a simple method of computing logarithms. It requires only a table of 100 numbers along with their logarithms.
Each one of these numbers is of the form ![]() e.g : 1.005
e.g : 1.005
The logarithm of a number is found by resolving the number into factors of the form ![]() and adding (or subtracting) the logarithms of those factors (which are kept in a small table).
and adding (or subtracting) the logarithms of those factors (which are kept in a small table).
e.g 1716 = 1000 * 1.1 * 1.2 * 1.3 so Log 1716 = 3 + Log 1.1 + Log 1.2 + Log 1.3
This is firstly an application of the simple definition : log (a * b) = log(a) + log(b).
However, to end the process, the number sequence is driven to a range where proportionality rules (the differences of the logarithms are equal to the differences of the given number).
This method is as old as the logarithms themselves, as we will see it. It resembles, in a sense, to the Prosthaphaeresis algorithm used in the 16th century and early 17th century to replace multiplication and/or division by addition and subtraction using trigonometrical formulae.
It was rediscovered -from time to time- by classical authors from 16th century up to the early 1960's where it has been adapted in a form usable by digital computers. Since then, it has been used widely in the internal algorithms used by calculators and computers.
The approach is efficient when the logarithm of an isolated number is wanted and no table available.
The "radix method" achieved success when electronic calculators arrived.
With their speed, re calculating a logarithm when needed was not an issue anymore.
The HP-35 used a silicon "radix table" comprising 10 numbers compare to the 100 radices of the Briggs table. Slower but who cares when an automat is doing the hard work. It also uses addition and shift operations only.
This article will cover the "radix method" in all its aspects and will start by an historical overview. It took me lot of research to put the pieces together : some details are buried in old books around the world.
The main references to the 'radix method' are
1 - Oughtred 1618,
2 - Briggs 1624,
3 - Robert Flower 1771,
4 - Zecchini Leonelli 1806,
5 - Thomas Weddle 1815
6 - Manning 1806,
7- Ellis 1881.
A very good chronological summary is in Ellis 'On the Potential Radix as a Means of Calculating Logaritlhms
1881'. But it does not cover Oughtred 1618, the very first appearance of the method in a text.
The method is very old and contemporary to the work of Napier.
It first appeared anonymously in an appendix to the english translation by E. Wright -1618- of the Napier's Descriptio.
Cajori had shown -by an analysis of mathematical notations- that the real author was very probably Oughtred.
It was next presented by Briggs himself in his Arithmetica logarithmca (1624) in chapter 14.
Briggs did not give details on how and for what purpose he used his Chapter 14 method : just another tool after many others.
He also gave no detail on how he calculated his 'radix table'.
Robert Flower in 1771 gave an outbreaking approach.
He was the inventor of the term 'radix' and he calculated a 23 places of decimals table.
He fully explained his method and how to compute the 'radix table'.
Leonelli 1806, followed Flowers (with radix table for natural log) ; his work is only a new approach of Flower's method.
Manning 1806 introduced potential negative radix (numers 0.9xx).
Weddle 1815 gave an original method, completely worked out, and the most important since Flower's.
Ellis 1881 proposed a positive and negative potential radix approach.
J.E. Meggitt April 1962 introduced "Pseudo Division and Pseudo Multiplication processes" which is an automated process similar to the radix method to compute log(x) among other functions.
1) Oughtred’s radix method.
"An Appendix to the Logarithms showing the practice of the calculation of Triangles, and also a new and ready way for the exact finding out of such sines and Logarithms as are not precisely to be found in the Canons."

Napier’s work on logarithms is found in two treatises, The Description of the Wonderful Canon of Logarithms and The Construction of the Wonderful Canon of Logarithms.
The Description was published in 1614 and the Construction, although written before the Description, was only published posthumously by his son Robert Napier in 1619.
• Mirifici logarithmorum canonis descriptio was published in 1614 (Edward Wright's English translation was published in 1616, the Appendix appears in the 2nd edition, 1618),
• Mirifici logarithmorum canonis constructio (1619) was written before the Description, but published posthumously.
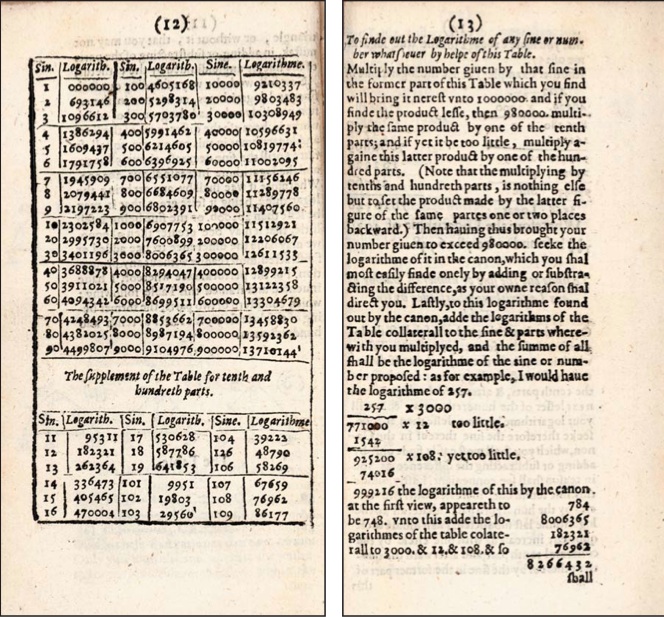
Below is a reproduction of page 12 and 13 of the Appendix of Napier's Description (1618).
Page 12 is the radix table itself and page 13, 14 and 15 the description of how to use it.
The appendix must be studied imperatively in the context of Napier's work.
Many authors thought wrongly, that the table of page 12 is the first natural logarithm table (base e).
It is not the case, as the text page 13 will prove it.
It is, in fact, an extension of Napier's short table §53 p.39 Mirifici Canonis "The construction of the wonderful canon of logarithms", with one decimal figure less (6 instead of 7) than in Napier's short table.
"Whence all sines in a ratio compounded of the ratios two to one and ten to one, have the difference of their logarithms formed from the differences 6931469.22 and 23025842.34 in the way shown in the following" short table (§53).
The sines with ratios 2 to one, 4 to one, 8 to one etc are tabulated.
It looks like a table of natural logarithms but it's only because the scaling factor has disappeared since the log of a ratio is taken :

e.g. 2 to one (5000000/10000000)
NapLog (5000000) - NapLog(10000000) = NapLog(5000000) = 6931471.80
by definition
NapLog(10000000) = 0
The author was not aware of the fact that he had built, in passing, a table of natural logarithms (base e).
Instead he introduced a concept of 'true logarithm' (p. 14) which base is virtually 1/e.
The Logs given in the Appendix (noted here Applog) have the same definition as in the Napier's short table but with a scale factor of 10^6 (one figure less).
The modern natural logarithm is equal to this 'true logarithm' subtracted from ln(1000000) * 10^6.
ln(x) * 10^6 = (ln(1000000) * 10^6) - TrueLog(x).
(see the Maxima file below).
But ln(1000000) is not even given in the table p 12.
With Maxima notation :
AppLog(y) := block([l],l:10^6 * log ( 10^6/y),return(bfloat(l)))$
The Appendix's table gives the 'AppLog' of each ratio :
e.g: for sine 2
AppLog(1/(2 * 10^-6)) ;
693147.180
In fact there is a lack of precision in the Appendix and sometimes errors.
How to use the Oughtred’s radix method?
The author gives an example (p.13) : "I would have the logarithm of 257."
- he brought the number close to 10^6 (in fact higher than 980 000 ; 10^6 is the whole sine) using the table and the supplement for tenth and hundred parts.
257 * 3000 * 1.2 * 1.08 = 999 216.
- he summed the logarithms found in the table log(3000)+log(1.2)+log(1.08).
Starting at around 980000 there is a proportionality zone where the difference of the logarithms are equal to the difference of the number : ln(x) < > x-1.
Going from 999216 to 1000000 requires a multiplication by 1.000784 or an addition (logarithm side) of 0.000784 because ln(1.000784) < > 0.000784.
The calculation is as follows:

Oughtred called this value (8 266 432) the 'true logarithm of 257'.
He almost discovered the natural logarithm.
ln(257) * 10^6 = ln(1000000) * 10^6 - True Log(257).
5549076 = 13815510 - 8266434
also
5549076 = AppLog(257)
13815510.5579 = Applog(1000000)
True Log = 8266434.4730
Note: AppLog(1000000) is not tabulated since natural logs were not known yet.

The second example is the given number 403.09 which is driven close to 1 (10^6) by 3 multiplications :
403.09 * 2000 * 1.2 * 1.03
reaching 996438.48
The logarithms to sum up are (from the table p 12)
log(2000) = 7600899
log(1.2) = 182321
log(1.03) = 29560
The difference is 3561.52 to top up the sum of logarithms 7812780 = 7816341.52 (Oughtred found 7816348).
Now the way around.
"Out of the logarithm given, subduct the logarithm of the former part of this Table, which is next less than it".
From the previous example:

1000000 - 784 = 999216
"which must be divided as is showed in the rule"
999216 / 1.08 / 1.2 / 3000 = 257
"So then the sine … is 257" (p. 15).
NB: The differences of the logarithms are equal to the differences of the sines until the sine has decreased from 10^6 (whole sine) to 980000 and the logarithm has increased to about 202000. (p 13 and p 14).
In this zone ln(x) ![]() x - 1.
x - 1.
For example 10^6/999216 = 1.000784615138268
ln (1.000784615138268) = 0.0007843074887246494
All calculations were made with Maxima :
(See the file here)