HP35 square root algorithm

Who remembers finding a square root using the traditional grade school method?

Happily, the so called  “longhand” process is engraved in the silicon of the HP 35’s ROM, and as long as collectors will keep the machine alive and working …

Let’s find (which happens to be 34) by the longhand process.

The traditional presentation is as follows:     

-    we mark off digits in groups of two,
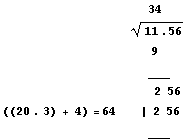-    we put under the number digits “11” the biggest square we can subtract 3 * 3 = 9,
-    we calculates the remainder 11 – 9 = 2,
-    we bring down the next group below the line drawn, 2 56,
-    now we compute  (left of the = sign) (20*3)+4 where 3  is the digit previously found and 4 is our best guess for the next digit, in this case 4,
-    b is chosen in order to make the remainder as small as possible ; in our example 64 * 4 =256 and 256 – 256 = 0,
-    the 2 digits (written above the radical are 3 and 4 and the answer 34.

The maths involved are easy. We note  and .
The iterative approximation consists in minimizing at each step the remainder.

Adding digit d to the current result (zero at the start) will lead to a new and smaller remainder ; let’s call the difference and if we note j the exponent of the power of 10 associated with the new digit d, we’ll have: or :

.

That’s precisely what’s going on in the longhand scheme above ().

Again, this process is described in J.E. Meggitt’s work (Cf. 1 p. 218), the pseudo quotients being chosen such that:

 as small as possible, and

, with the following recurrence relations:

 (equation 41 and 42).

The designer kept this scheme but re-worked a bit the delta remainder expression to have a simpler automaton.

An ancient theorem says that the sum of the first n odd numbers is the square number:

if we add both expression, we have :

 and finally .

Let’s rewrite the delta remainder formula; it comes:

with ,

where k is the rank if the first d odd numbers,

That’s the mathematical scheme of the algorithm but in fact, for a simpler implementation, the designer will retain the  expression:

 with .

In the following tables:

           A       B       C                    

Now, let’s get back to our example of  and let’s look close at the algorithm implemented (see please the trace of the example)

The square root key will, after a few relays, branch to the “sqt14” label, with argument X in register A and B and pointer P initialized to 4 [BP1],

We enter here in a loop preparing registers for the core routine,

-  P being initialized to 4, we are looping 5 times and adding A 5 times to itself, calculating 5 times the remainder, 

- instruction “sqt14”  c + 1 -> c[s] executed five time, will set the 13th digit of C to 5, we have seen above why,

 -  a test to carry is made at address 1275, to test the error condition  of a square root of negative argument (if carry we go to 0277 to blinking display) [BP2],

 - the exponent of A is added to itself (multiplication by 5) at label “sqt18” to test further easily if even or odd [BP3],

 - another test to carry is done at address 1334 [BP4] after doubling the exponent: if exponent is negative then instruction c – 1 -> c[p] will put a digit “9” in good position in register C to make the final negative result exponent (at address “sqt13”).

 




Finally, all is set up at address 1342 [BP5] where :

- mantissa is 5 times the argument is in A,
- its exponent is in C,
- digit 5 is the at 13th position in C. 

1) Exponent processing

At address 1343 a test is made on digit zero of register C: is it  = 0 or >=1 ? [BP6]

This is another benefit of the multiplication by 5 trick.

Let’s write the argument in floating point form.

If the exponent is even the square root is = , but if it is odd, the mantissa has to be shifted right and the exponent to be incremented, to keep the number the same.

But the designer sought a way to avoid the division by 2.

The trick is simple, in the process of multiplication by 5 of argument, he involved the exponent: so we have, entering the core routine:  instead of.

The test is now easy: an odd exponent will end with digit “5”, and even with digit “0”, and more a single shift right on register C that holds at that time the exponent is doing the trick [BP7] (this SL at address 01346 is also dealing with negative exponent – see above):

                        Argument exponent                x 5                     result exponent after SR

                                   0                                 0                                 0
                                   1                                 5                                 0
                                   2                                10                                 1
                                   3                                15                                 1
                                   4                                20                                 2
                                   5                                25                                 2                                

that turns out to be the final answer exponent.

2) Fraction part processing

We cannot process the mantissa without taking into account the exponent. In fact, fraction parts follow a modulo 2 cycle: 

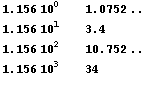
Normally, for an even exponent a shift right of register A is needed. But here, the digit 5 in register C is already in a fixed place (digit 11) when entering in the loop at label “sqt17” [BP8], and will go further, at the start of the core routine, to the 13th place in register C.

Now, here is a crucial point: we have to take care of the alignment of the fraction part of A and of digit “5” in the C register:

A: [0 5 7 8 0      ]
C: [0 0 5           ]
     13 12 11

In the “odd” case, it turns out that both numbers are already aligned, that is why the test at address 01343 is inversed: if exponent is even (exponent ending with a digit “0”), we will shift register A one place to the right (address 0145).

This process sqt15 -> sqt16 -> sqt 17 is done until p=0 that is to say when 12 bits have been computed, even if there is nothing left to subtract.

At the very end, we go to normalize the result (label “tnm12”): result exponent is appended to the calculated mantissa in C (address 01056).

This final implementation is robust and fast.

J. Laporte
January 9, 2006.

1) J.E. MEGGIT, Pseudo Division and Pseudo Multiplication processes, IBM Journal, Res & Dev, April 1962, 210-226.