Output format

Output format routine

The task of the "output format" routine is to build the display context and to call the "dsp" routine to loop displaying the previous result and waiting for a key.

It is the main return point from mathematic routines: after the result has been "normalized" in the C register, a call to "of13" is made.

00333: jsb of13
            1 -> s7
fst2zx: jsb dsp1
            jsb fst3
            go to den2

Note that when entering digits, “of13” is not called: the “den” routine will take care of updating the display mask.

The routine has 2 other entry points:

1) at power on (PWO) or when the CLR key is pressed, the control branches to address 00000, a "clears registers” is executed and a call to "of12" is made,

2) when the key CLx is pressed, the control branches at address 00070 and the call to "of12" is made without executing "clears registers"

00067: clear registers
jsb of12
00071: go to fst2zx

Note that entering at "of12" causes the C register to be zeroed, that's the difference between the 2 clear keys: CLR is clearing all the registers while CLx is just clearing the display X (C register).

1) Display context

I have already explained that, a 56 bit register in the A&R, holds 14 BCD digits (10 mantissa digits, 2 exponent digits and 2 sign digits).

Three registers A, B and C are dedicated to hold the display information, while the machine is in the display context, that is to say, while looping in the "dsp" routine.

Elsewhere, in a math routine for instance, the A, B and C registers can be used freely by algorithms.
One restriction though due to the instruction set, only register A has a shift left capability.

Note that the decimal point appears at the right of the most significant digit (12th).

The sign of the fraction part (mantissa) is coded with the digit “9” when negative (“-“) and “0” when positive (“+”).

In the normalized C register, the exponent is coded in tens complement notation, so that the number is represented in normalized form as C=91250000000998.

On exit of a math routine, the result is held by the C register and routine "nrm" is called to build the normalized for of the result in C and at the end of "nrm" a call to "of13" is made (address 00333) to build this "display context" before going into "dsp" to display the result and wait for a new key.

The HP35 (and later calculators) uses 3 registers to represent a number:

- register C holds the normalized form,
- register A has the displayable form (floating point),
- and register B holds a mask to correctly position the decimal point.

With this scheme the decimal point does not need a register position and the machine as both a floating point and a normalized format at a small expense of ROM space.

In fact, the A register is set up to hold the display in floating point format and its digits are in proper order while the B register is used as a masking register with digit “9” for each digit position to be blanked, digit”2” for the decimal point position and digit “0” for displayed digit position.

This information is used by the cathode and anode driver hardware when the BCD digits in register A are gated into display, the mask in B is used to OR correctly the digits to be blanked and the decimal point.

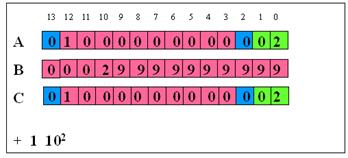
In the example above the number 100 has been return by the multiplication routine as 10²:

But -and it is an innovation of the HP35- results between 10¹⁰ and 10^-2 will always be displayed with the decimal point properly positioned and the rest of the display blanked.

Otherwise, as stated in the user manual (p.22) answers are displayed in “scientific notation”.

The machine has to handle the 4 display format cases:
1) results as 10²to be displayed as “100.”:
(registers on entry in “of13”)
A=01000000000002 B=00029999999999 C=01000000000002

2) results as 10^-2 to be displayed as is “.01”

A=00100000000902 B=20099999999999 C=01000000000998

3) results to be displayed in “scientific notation” has 1 10¹²,

A=01000000000012 B=02999999999000 C=01000000000012

4) results to be displayed in “scientific notation” has 1 10^-12,

A=01000000000912 B=02999999999000 C=01000000000988

Note, the special format of results -in the cases of “overflow” and “underflow”- are handled by the “of” routine:

- overflow: 1 10⁵⁰ * 1 10⁵⁰ display = “9.999999999 99”
A=10000000000500 B=02999999999000 C=01000000000050

- underflow: 1 10^-50 * 1 10^-5 display "0"
A=10000000009500 B=02999999999000 C=01000000000950

(see trace).

2) "Of13"

The code starting at label "of13" is the common part. It can also be entered at "of14" from eex8, when the EEX key is pressed first (see in the “Data entry” article)

These multiple entry points explain some kind of redundancy in the code:

of12:    0 -> c[w]
of13:    clear status
           c -> a[w]
           c -> a[x] ...etc..

"Of13" starts by a "clear status" which set all status bits to zero, then as it’s going to work out the data on C, its value is saved in A and B (both exponent of a and b will be added to determine over or underflow, see below), so on entry normalized and floating point forms are identical; the rest of the routine will differentiate them.

At address 00142, the sign of the exponent of C is tested: if it is different of 0 (# 0), we have 3 cases:

- real negative exponent (e.g. -6 is exponent 994).
- overflow condition from the math routine "100",
- underflow condition form the math routine "900".

To filter the 2 last cases, we take nines complement (address 00144, 00145)

- real negative 994 will be 906 (floating point -6) with a carry,
- overflow 100 will be 800 with no carry,
- underflow "900" will be "000" with no carry, and we test the carry at 00146.

So in the over or underflow we go to "of11" to build the proper display (see this trace for details).

3) Of11

To build the future number to display in overflow (display "9.999999999 99") or underflow (display "0.") the code will:

-         - put zero in c[wp] (p=12 since "of14"),
-   subtract 1 (C="09999999999999"),
-   and zero c[xs] the result is C="09999999999099".

We have to determine if we are in an overflow condition by adding a and b exponents (doubling result exponent in fact) ; if there is no carry (100+ 100 = 200) we go again to "of13" with the "overflow" normalized display in C.

If carry (900 + 900), that was an underflow and we go to "of12", zeroing register C and we fall through "of13".

4) Of15

We can arrive here by two paths:

1- if the exponent sign of C is zero (zero or positive exponent) after the test at 00142,
2- or in case of a normal negative exponent (no under or over flow case),

In the later case, the pointer is changed to 5, due to the fact that numbers < 10² must be displayed in scientific notation.

The instruction at 00150 (a <-> c[x]) restores C with the normalized exponent form (complemented) and A with the floating point form: if we came from 00144 (normal negative exponent), there is a difference: e.g. if the exponent is -2, A holds now 902 and C = 998.

Next we test status bit S4 to see if EEX key has been pressed:

- if no we go to 00102, it's the normal path,
- if the “EEX” key has been pressed, see in the “Data entry” article explanations about "eex" the code between 00153 and 00157 is part of the eex3 routine.

5) Display mask building

Now I have to describe the most important part of the routine (0102-0113, 0341-0361) which task is to build the display mask from normalized data in C

The entry point of this routine is at address 152: we normally go to 102.

We first save A to work out on it, reset its exponent sign to zero and we shift A one position left to be able to decrement the unsigned floating point exponent.

Then at address 00105 we decrement a[x] which is the floating point exponent.

If we decrement it one step overmuch, a carry will be raised the result an exponent “999” in A and we will continue in 107.

But if the result is still positive we will go immediately to 00340.

In the loop 00340 – 00105, register A is going to be shifted right (00340), its exponent is decremented (at 00150) and the pointer p is decremented (00341):

- until p = 2 or,
- until there is a carry at 00106.

It is easy to guess that this loop is doing the conversion between normalized form (on entry A=C) and scientific notation. In fact it is the loop that makes the decimal point floating.

On entry in the loop the pointer p = 12 and there is an exit door at 00342 when p will be = 2, so we have two distinct paths to exit the loop:

- at 00344 (p = 2), we could decrement the pointer p 10 times and the decremented floating point exponent is still <> 0 : we are in the case of a result in the scientific notation range > 10¹⁰- at 00107 on the contrary the floating point exponent has been decremented to zero before the pointer p has reached the value 2: we are in a case where the number must be displayed in a fix format with the decimal point properly positioned.

1) On exit at 00344

Pointer p is set to 12 and A is zeroed (the mask is built in A and will later be exchanged),

At 347 and 350 a digit “2” is put at the current p location:

a + 1 -> a[p]
a + 1 -> a[p]

the mask is then “02000000000000”, the pointer is reset to 2, and the mask will be fill from position 3 (at 00353) with digit “9” up to the first significant digit in B.

If we have gone a step too far; we reverse gear (at 00357) and exchange A and B.

At the end of process, the mask is in B = “02999999999000” in the example of 10¹².

2) On exit at 00107

A has been decremented until floating point exponent is 999 and until there is a carry at 00106.
Pointer p has a value between 2 and 12: for example if the result is 10⁵ then p = 7 and the number will be displayed as « 100000 », with a mask = “00000029999999”.

2.1) At 00107 we test if exponent is zero or positive and if yes we go to 00346, zero mantissa and sign of register A (=00000000000999) and we put a digit “2” in the current position pointed to by p.

Next as above, the pointer is reset to 2, and the mask will be filled from position 3 (at 00353) with digit “9” up to the first significant digit in B.
At 00357, we have gone one step to far, we reverse gear and exchange A and B.
The built mask is in B (“00000029999999).

2.2 If normalized exponent was < 0 at 00107, we are in a the case of numbers as 10^-2

that must be displayed as “.01”, the decimal point first.

The mask to construct has the form “20....”, that is why at 00112 the pointer is set to 13 before going to 00346 to build the rest of the mask (see the trace file for details).

Note that, the exponent display is blanked (mask = 999) if exponent of register A has been decremented to -1 ; i.e. if we came to 00346 by the 00107 or 00113 paths.

On the contrary, exponent is displayed (mask = “000”) if we came to 00346 by path 00342 (p = 2).

Note also that a negative exponent > 10 (for example -12) is treated as a positive due to instruction 00104, the original value being saved at 00102.

In that later case, numbers > 10^-2will be displayed in scientific notation, since p was set to 5 before entering in 00102 (see address 00147) allowing only 3 (5 – 3) decrements of A.

This code was a little bit hard to understand.

The only method that was able to put some light on it was predictive reverse engineering.

You must first reverse the specifications, and imagine what the designer wanted to do.

J.Laporte
Thursday, 23 February 2006