THE BUGS in early ROM - 2
The “arc tan” flaw etc ….
Good hunting last month, so I took the same gun this time.
I replaced in the “hp35.lst” ROM file running in the simulator “sim35” the two lines:
396 L01117: 1.11.1.11. shift right a[ms]
397 L01120: 1.11..1..1 -> L01262 jsb div14
by the following:
396 L01117: .1111...1. c + 1 -> c[p]
397 L01120: 1.11.111.1 -> L01267 jsb 1267
These instructions are the only to be modified in the new HP 35 ROM, in the inverse trigonometric routines.
This patch made, all the bugs in the inverse trigonometric functions reappear.
Now the explanation, known that the two codes work well in 99% of the cases.
1) Cordic reminder.
The problem occurs for certain cases listed in the errata
sheet, in the “Trigonometric functions” paragraph; let’s take the first case arc
tan 0.0002.
Please, refer to what I wrote last December about the inverse trigonometric
functions.
We start from a point (X,Y), X=1, Y=0.0002 and make “vectoring” rotations to minimize the Y component, then we try to make as many rotations as possible for each angles in ROM: arctan(1), arctan(0.1), arctan(0.01), arctan(0.001) and arctan(0.0001) and we store the number of possible rotations for each constant (we stop if we have a negative result).
2) The arc tan flaw
I own a “buggy” Rom machine for almost 30 years! As you can think, I’ve done in the past experiments on that bug, which was referenced in the errata sheet sent by HP.
When you enter 0.0002 and push the two “arc” “tan” keys, the result is 5.729577893 10-3 .
I always thought this angle (in
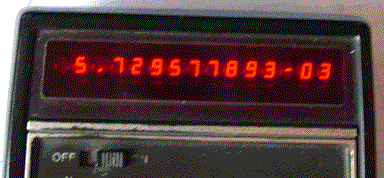 degrees)
was puzzling since converted in radians it is just 0.0001.
degrees)
was puzzling since converted in radians it is just 0.0001.
I thought that some factor had been forgotten, but I just
bought another debugged machine, kept the old one as a future rarity and time
passed.
March 2006, I get on my desk the 2 paper traces of the same calculation on the 2
ROMs and as a bonus the answer to the mystery.
At the level of accuracy of the HP35’s Cordic implementation, the real number 0.0002 leads to a strange pattern:
arctan(1) : no rotation possible,
arctan(0.1) : no rotation possible,
arctan(0.01) : no rotation possible,
arctan(0.001) : no rotation,
arctan(0.0001) : only one Cordic rotation and that’s all.

So far so good, the pseudo quotients of the calculation are “00001” and since there is not much work we can do right away the rest of the calculation.
After the only rotation of angle arctan(0.0001), the
components are:
X= ![]() and
Y=
and
Y= ![]()
and the remainder r=Y/X from which we are going to start the « pseudo
multiplication » is r = ![]() .
.
The rest is straightforward since there is only one rotation,
we need to add to r, one time the constant arc tan(0.0001) , the result being
![]() and
converted to degrees =
and
converted to degrees = ![]() ,
which happens to be the good result.
,
which happens to be the good result.
We have also easily the key of the mysterious bug ; if we forget the
remainder r and equate it to zero ; our result is simply 0.000099999997 which
converted to degrees gives the arc tan flaw: 0.00572957…
The careful study of the patient’s file gives a limpid
diagnosis: the flaw
is not in the pseudo quotients (part 1, Cordic rotations), and not in the second
part (pseudo multiplication and conversion to degrees).
Then where is it? HP 35 is unable to make Y/X to calculate the remainder …but
the code works most of the time.
“ If anything can go wrong, it will”
(Murphy's law).
Back to the “floating point division” file and back to school. Where is the
damned file? A couple of hours minutes later, I have the flow chart under
the eyes.
Something is clear, if I can say, the entry point is not the usual one (see
please my paper on floating point division).
The original errata sheet (photo J.Laporte)
Most of the time, in the HP35 ROM, the entry point for the “division” routine is “div11” (address 1246) and the call is “jsb div11” which will in turn call the core divider “div 14”.
This time and only in the inverse trigonometric routine the code path is not the regular one, and if you look close the difference is not small.
The first way (call to “div11”) takes two normalized numbers, mantissa and exponent, and prepare them to the operation whereas the core divider (“div14”, “div15 etc) just subtracts aligned mantissas and stores the result in C (via the instruction c + 1 -> c[p] – where p is the number of time the subtraction could be repeated).
Probably due to a lack of space, the designer chose to dive directly into the core division routine at address 1267, just before the end of the loop (see chart below).
Pointer p that holds at that moment the value 12, is just decremented and we loop to “div15” to perform the normal cycle of the division by repeated subtractions. This part of the algorithm is easy to understand.
What is more difficult to catch is the reason why the 12th position of register C is forced to one, before the dive.
Since both numbers in the division Y/X were not prepared (normalized), it is mandatory that the result is kept untouched by the normalization routine on exit (a flag would do the trick but alas …), and to avoid the left scaling of non significant zeroes (at label “nrm23”).
That’s the reason of the instruction c + 1 -> c[p] before the call “jsb 1267”.
Note that the jump address saves one subtraction and one shift left (address 1263 and 1266), so that normally mantissas are still aligned, and the result unchanged.
To show how this code works in normal cases (most of the time) : I have linked two run traces arctan(20) with the new ROM and with the buggy instructions.
The result of the division will be forced to 1 at the12th rank in register C and that digit will be removed by the first instruction after the return: the division result (number of times) will start to increment the 11th digit of register C.
01120: jsb 1267
01121 c - 1 -> c[p]
Now what went wrong?
In our case, the single trace speaks by itself.
We have to divide A/B by repeated subtractions: (A=00100000000000, B=00010000000000).
01263 div15: a - b -> a[ms]
A=00090000000000 B=00010000000000 C=01000000000000
P=b Digit 12 forced to 1 before entry
01264: if no carry go to
div14 at
1117,
A=00090000000000 B=00010000000000 C=01000000000000 P=b
01262: .1111...1. div14: c + 1 -> c[p]
Y/X (A/B)
A=00090000000000 B=00010000000000 C=01100000000000 P=b
one time
01263: div15: a - b -> a[ms]
1 subtraction
A=00080000000000 B=00010000000000 C=01100000000000
P=b accumulated in the 11th digit
01264: if no carry go to div14
A=00080000000000 B=00010000000000 C=01100000000000 P=b
01262: .1111...1. div14: c + 1 -> c[p]
2 times, 2 subtractions
…/… etc up to 9 times
01262: .1111...1. div14: c + 1 -> c[p]
9 times
A=00010000000000 B=00010000000000 C=01900000000000
01263: 11...1.11. div15: a - b -> a[ms]
A=00000000000000 B=00010000000000 C=01900000000000
01264: 1.11..1.11 -> 01262 if no carry go to div14
A=00000000000000 B=00010000000000 C=01900000000000
01262: .1111...1. div14: c + 1 -> c[p]
10 times!
A=00000000000000 B=00010000000000 C=01000000000000
dividing 0.1/0.01 with this code
01263: 11...1.11. div15: a - b -> a[ms]
the overflow will occur only at the
A=99990000000000 B=00010000000000 C=01000000000000
11th subtraction:
01264: 1.11..1.11 -> 01262 if no carry go to div14
A=99990000000000 B=00010000000000 C=01000000000000
we lost one digit
the partial result
is a flaw: 1 instead of 2
There are two concurrent causes for this wreckage:
- the unusual case we’re in, having to divide 0.0001 by 1.0000000 (the mantissa being aligned as A=00100000000000 and B=00010000000000,
-
and the jump into the code made right
in the middle of the division routine (jsb 1267) ; thus the shift left a[ms] at
1266 is not executed and the code can make 11 subtractions (see
above) causing an overflow that leads –at the end- to register A being
zero : A=00000000000000.
With this simple little flaw in the division implementation the remainder r in the arc tan(0.0002) case is ZERO, which in turn added one time to arc tan(0.0001)= 0.000099999997 and converted to degrees gives the arc tan flaw: 0.00572957…
3) The cure
Ok, now the cure.
This time the designer did a regular call to routine “div14”:
- he shifted right the A register (dividing it by 10), taking thus into account the 12th digit forced to 1, by routine “div14” ; this does not affect the result, since “div14” routine will do a shift left at address 01266 (see the trace of arctan(20) on the new ROM),
-
then he just called “div 14” ; on
return instruction 01121 will remove the digit forced to 1 in this routine at
address 01262: c – 1 -> c[p].
That’s only two faulty instructions:
01117: c + 1 -> c[p]
01120: jsb 1267
to replace by:
01117: shift right a[ms]
01120: jsb div14
And the nasty bugs disappear.
Jacques Laporte
07 April 2006
Ps1: I link the two traces for arctan(0.0002) on the new rom and on the same rom with the 2 faulty instructions.
Above is the explanation for the flaws listed in the errata sheet HP sent, at point 1, 2 and 3: enter 0.0002 the press “arc” “tan” or “arc” “sin”, etc.
Ps2: Another Murphy's Law :
”Things get worse under pressure.”
At point 3: there is an error (typo) in the errata sheet !
If I enter on my “buggy” machine “0.7071774882” “arc” “sin”, it gives the good
result 45.00572955 (In fact I just cannot enter the last digit “2”!).
Only the following entry –without the leading “0” -gives the faulty result
“.7071774882” “arc” “sin” or “arc” “tan” (.707… and not 0.707.. one more digit
internally).
Murphy's Laws from the site http://www.murphys-laws.com/murphy/murphy-laws.html
