Here are the tools
I used, in 2004-2005 and 2006, to study the ROM and complete my notes and here are the names of
the people I’m glad to thank.
Peter MONTA realized the
dump of the HP-35 ROMs optically! You must study is genial optical way of
dump the ROM 3 x 2560 bits arrays using a light source to reveal contacts
representing a "1" bit, and no contact representing "0".
Eric SMITH, wrote CASMSIM
http://www.brouhaha.com/~eric/software/casmsim/ an assembler and simulator
for the HP 35 (and other HP Classic calculators ) later replaced by
Nonpareil (see his paper
Microcode-Level Calculator Simulation PDF, presented at the HHC 2004
conference in San Jose, California on 26-SEP-2004).
Finally, David G. HICKS wrote a java version of the
Smith’s HP 45 emulator (available on his famous site
Museum of HP Calculators
http://www.hpmuseum.org/simulate/sim45.htm. This applet simulates an HP-45
running the actual
HP-45 firmware.
I worked with the late version, modified it to
make it compatible with the HP35 format and ROM listing, disassembled by E.
SMITH from the dump by P. MONTA, and finally added it a trace capture capability
(all modifications under
GNU General public licence
Version 2, June 1991). Therefore, the source
file is available here.
I validated the ROM listing comparing results (lack of
precision in some cases) with my real machines and finally (summer 2006) I dumped myself
electronically a HP 35 ROM ( type 2, SN 1212313213).
All traces available on these pages are made with this
ROM simulator tool that reproduces every result given by my old HP35 (even if an error) so I
could do all my sample calculations, step by step. You can use this
tool yourself, launch a calculation, capture the trace
(code listing and registers), copy, past it in an editor (it's a Java applet!)
and finally print it for later study.
Peter MONTA dumped also very
recently (Feb 2006) the early ROM with bugs (many thanks to him): you can
experiment here on this ROM. Since then, I have
fully elucidated the famous "exp(ln (2.02))=2" bug (see my page
about the BUGS in HP 35 early ROM).
The algorithms discovered and explained with
these tools are the same described in the original papers by MEGGITT, VOLDER,
& COCHRAN.
I now give -in the pages of this web site- a step by step comment of the totality of the HP35 ROM.
The interest is not
only historical but of great value for understanding hardware numerical method
used in small calculators; at that time and still now.
Before diving in
the main topic, I must introduce a minimum of notions about
- HP 35 Arithmetic and Register (A&R) architecture and programming code,
- ROM listing (object code has been dumped from real ROMs
and assembler labels -which are unknown- have been copied from the HP45 Patent
n° 4001569),
- Relation between
key codes and subroutines addresses.
I cannot cover
presently and here all aspects of HP 35
hardware technology (but I hope to do it in the year 2006). Many details can
however be found the
Museum of HP Calculators.
However a few points of the programming model must be kept in
mind, to be able to read the trace of the functions.
1) The HP-35 programming
model
The HP35 has a
serial architecture (a one line bus) and his arithmetic and register CPU is made
of 7 registers of 14 words each to handle floating point numbers.
Each digit or sign
is 4 bits large using Binary Coded Decimal (BCD) encoding (http://en.wikipedia.org/wiki/Binary-coded_decimal)
(in BCD “9” is
coded “1001”, “10” is “0001” “0000”, “11”is coded “0001” “0001” etc .)
With this scheme it is very simple to drive the 7 segment LEDs.
Each register, in
the HP35, consists of 14 of 4 bits each that is to say 56 bits: 10 digit of
mantissa, a 2 digit exponent and signs for the mantissa and exponent.
Some registers are
known by the user by the names of X, Y, Z, and T and represented the operational
stack X (display), Y, Z and T (top of the stack).
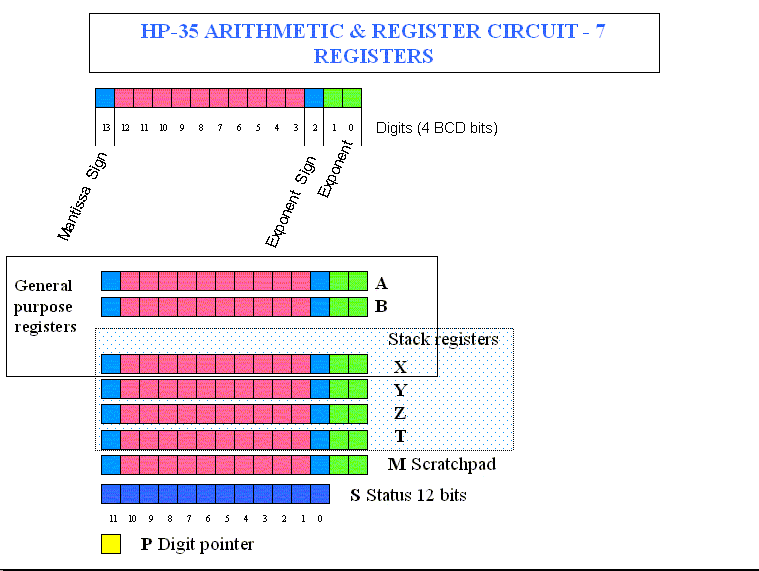
Technically, in the
ROM mnemonics, they were named differently (here I use and adapt David G. Hicks’s work):
- A, B: General
purpose registers,
- C: Display,
- D, E, F:
operational stack levels Y, Z, and T,
- M: scratchpad
register (transfers to and from the C register),
- P: 4 bit
"pointer" register used for register field addressing (offset into the
registers),
- S0-S11: 12 bits
of programmable status.
Operations with a field select option
allow part of each register to be accessed.
|
M |
Mantissa |
|
MS |
Both mantissa and Sign |
|
X |
Exponent |
|
XS |
Exponent Sign |
|
S |
Mantissa Sign |
|
P |
Pointer
|
|
W |
Word (the 14
digits of the specified register) |
|
WP |
Word up to the
nibble pointed to by P register (if P=3, WP would refer to nibbles 0, 1, 2,
and 3). |
The sign nibbles
are set to 0 if positive and 9 if negative.
2) Addressing &
Instructions
The HP35 used 8 bit
instruction addresses plus ROM select instructions to activate the appropriate
256 word ROM. Portions of
registers to act on are indicated by enclosing the field select code in brackets
[]. Each instruction
occupied 10 bits (256 x 10 = 2560 bits).
Here again to
present the instruction set, see David G. Hicks for
more details. I’ll focus on
examples taken in the object code listing of the HP35 ROM.
|
field |
field select (
M, MS,X, XS, S, P W, WP.) |
|
register |
general purpose
register (A,B, C) |
|
label |
a label |
|
bit |
a value of 0 or 1 |
|
digit |
a value between 0 and 9 |
|
status |
a status
register bit number (0 - 11) |
|
pointer |
a pointer value (0-13) |
|
rom |
a ROM number
(max depends on model) |
Clearing
|
CLEAR REGISTERS |
Clear (zero)
all 56 bit registers |
|
0 -> register[field] |
Set the
selected field of a register to zero. |
|
CLEAR STATUS |
Clear (zero)
all 12 status bits |
This is the CLR key routine and the PWO
boot:
89 L00067:
111.1.1... l00067: clear registers
90 L00070: .1.111... 1 -> L00134 jsb of12
132
L00134: ..11..111. of12: 0 -> c[w]
133 L00135: ....11.1.. of13: clear status
Register
copy to register
|
A -> B[field]
B -> C[field]
C -> A[field]
M -> C
C -> M |
Copy the
selected field of the origin register to the field of the destination
register
|
e.g.
The entry point for e^x ln log or x^y
02010: .11...111. c
-> a[w]
A=04400000000000 B=02099999999999
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
Register C (display) that contains the
ln(x) argument, number 0.44 is saved in register A field W (entire word)
A few steps further:
02013: 1.111.111. 0 ->
a[w]
A=00000000000000 B=02099999999999
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
The simulator gives the instruction in
object and symbolic and the result of execution in A, B, C, D, M registers and
also in the Pointer P and Status Bits (bits 0, 2, 6, 7, 8 9 are SET while others
are reset).
Another example using field and pointer
addressing (before and after execution):
A=01120000000000 B=00560000000000
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02024: 11.11...1. a -
1 -> a[p]
A=00120000000000 B=00560000000000
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
Register A is decremented at the field
pointed to by P (12) and the result is stored at he same address.
Register
Exchange
|
A EXCHANGE
B[field]
A EXCHANGE C[field]
C EXCHANGE B[field]
C EXCHANGE M |
Exchange fields
of the two registers.
C<>M always on full word. |
e.g.
02331: 11...11111 -> 02307
then go to mpy28
A=01481604541800 B=00000000000900 C=09900000000000
D=00000000000000 M=00000000000000 P=c S=0.2...67.9.b
02332:
111.1..11. a exchange c[m]
A=09900000000800 B=00000000000900 C=01481604541000
D=00000000000000 M=00000000000000 P=c S=0.2...67.9.b
Register A
mantissa is exchanged with C counterpart
|
Register
Arithmetic
A + B ->
A[field]
A + C -> A[field]
A + C -> C[field]
C + C -> C[field]
A – B -> A[field]
A – C -> C[field]
A – C -> A[field] |
Perform
arithmetic on field |
|
A + 1 -> A[field] |
Increment field |
|
C + 1 -> C[field] |
|
|
A – 1 -> A[field] |
Decrement field |
|
C – 1 -> C[field] |
|
|
-C -> C[field] |
Negation of C
(10s complement) |
|
-C -1 -> C[field] |
Negation of C
and decrement (9s complement) |
e.g. eca22 routine
02023: 1..1.11..1 -> 02226 jsb eca22
A=22232000000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02226: 11.111111.
eca22: a - 1 -> a[s]
A=12232000000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000 P=c S=0.2...6789.b
Mantissa sign of register A is
decremented.
Register
Shift
|
SHIFT RIGHT
register[field] |
Shift selected
portion of register to the right |
|
SHIFT LEFT
A[field] |
Shift selected
portion of A to the left |
02227: 1..1.1.111 -> 02225 if no
carry go to eca21
A=12232000000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02225: 1.11.1..1.
eca21: shift right a[wp]
A=10223200000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000 P=c S=0.2...6789.b
Routine eca21
Part of the A register (from 0 to 11 – P=12) is shifted right.
Register
branching
|
IF B[field] = 0
IF C[field] = 0
IF A >= C[field]
IF A >= B[field]
IF A[field] >= 1
IF B[field] >= 1 |
Test for
selected part of register (THEN GO TO) |
|
THEN
GO TO label |
Go to label if
true |
|
GO TO label |
Unconditional go to |
|
IF NO CARRY GO TO label |
Go to label if
carry bit is not set |
02226: 11.111111.
eca22: a - 1 -> a[s]
A=00223200000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02227: 1..1.1.111 -> 02225 if no
carry go to eca21
A=00223200000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02225: 1.11.1..1.
eca21: shift right a[wp]
A=00022320000000 B=22232000000000
C=11144000000000
D=00000000000000 M=00000000000000 P=c S=0.2...6789.b
In eca22, if
operation decrementing sign of A does not generate a CARRY then GOTO eca21.
Status
testing
|
bit -> status |
Set status bit
(eg: 1 -> S10) |
|
IF status = 0 |
Test if status
bit equal to 0 |
|
IF status # 1 |
Test if status
bit not equal to 1 ) |
At the very start of the ln routine, a
test to status bit S8 is done ; if S8=0 then branch to exp(x) routine. It is in
fact the entry point for e^x, ln, log or x^y.
02011: 1....1.1.. if s8 = 0
A=04400000000000 B=02099999999999
C=04400000000000
D=00000000000000 M=00000000000000 P=c S=0.2...6789.b
"pointer"
register setting
|
pointer -> P |
Set P register
to pointer (pointer nth nibble for P field select or through pointer for WP) |
|
P + 1 -> P
P -1 -> P |
Increment and
decrement pointer P |
|
IF P # pointer |
Test if P not
equal to pointer (follow with THEN) |
In prologue to ln(x), set P to 12.
00137: 11....11.. of14: 12
-> p
A=00000000000000 B=00000000000000
C=00000000000000
D=00000000000000 M=00000000000000
P=c S=............
Stack
operations
|
C -> STACK |
Push C onto the
stack (E->F, D->E, C->D) always whole word |
|
STACK -> A |
Pop stack into
A (D->A, E->D, F->E) always whole word |
|
ROTATE DOWN |
Move D to C, E
to D, F to E and the original C to F (just like pressing the Roll Down key.) |
Subroutine
call
|
JSB label |
Jump to
Subroutine label (one level of subroutines) |
|
RETURN |
Return to the
instruction after the JSB. |
02023: 1..1.11..1 -> 02226 jsb eca22
A=00560000000000 B=00560000000000
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
02226: 11.111111.
eca22: a - 1 -> a[s]
A=90560000000000 B=00560000000000
C=04400000000000
D=00000000000000 M=00000000000000
P=c S=0.2...6789.b
Miscellaneous
|
LOAD CONSTANT digit |
digit -> C at
the Pth nibble. P is then decremented so multiple digits can be loaded
easily. |
|
SELECT ROM rom |
Select ROM #rom
for addressing. |
|
KEYS -> ROM ADDRESS |
Jump to the
offset of the current keycode in the currently selected ROM. |
|
DISPLAY OFF |
Turn the display off |
|
DISPLAY TOGGLE |
Toggle the LED
display on/off. |
|
NO OPERATION |
Place holder doing nothing. |
Here we load the constant ln(10) = 0230258509
02366:
..11..111. lnc10: 0 -> c[w]
A=00820980552045
B=44000000000000 C=00000000000000
D=00000000000000 M=00000000000000 P=b S=0.2...67.9.b
02367:
11....11.. 12 -> p
A=00820980552045
B=44000000000000 C=00000000000000
D=00000000000000 M=00000000000000 P=c S=0.2...67.9.b
02370:
..1..11... load constant 2
A=00820980552045
B=44000000000000 C=02000000000000
D=00000000000000 M=00000000000000 P=b S=0.2...67.9.b
02371:
..11.11... load constant 3
A=00820980552045
B=44000000000000 C=02300000000000
D=00000000000000 M=00000000000000 P=a S=0.2...67.9.b
02372:
.....11... load constant 0
A=00820980552045
B=44000000000000 C=02300000000000
D=00000000000000 M=00000000000000 P=9 S=0.2...67.9.b
Here we have
pressed the LN key so we go offset 00003 (see table below).
00330:
..11.1.... keys -> rom address
A=44000000000000
B=02099999999999 C=04400000000000
D=00000000000000
M=00000000000000 P=c S=0.....678..b
00003: .....1.111
-> 00005 go to l00005
A=44000000000000
B=02099999999999 C=04400000000000
D=00000000000000
M=00000000000000 P=c S=0.....678..b
|
"CLR", |
0 |
|
"e^x", |
2 |
|
"ln", |
3 |
|
"log", |
4 |
|
"x^y", |
6 |
|
"RCL", |
10 |
|
"STO", |
12 |
|
"Rdwn", |
13 |
|
"x<>y", |
14 |
|
"1/x", |
16 |
|
"6", |
22 |
|
"5", |
23 |
|
"4", |
24 |
|
"+", |
26 |
|
"3", |
32 |
|
"2", |
33 |
|
"1", |
34 |
|
"x", |
36 |
|
"Pi", |
42 |
|
".", |
43 |
|
"0", |
44 |
|
"/", |
46 |
|
"tan", |
50 |
|
"cos", |
52 |
|
"sin", |
53 |
|
"arc", |
54 |
|
"sqrt(x) |
56 |
|
"9", |
62 |
|
"8", |
63 |
|
"7", |
64 |
|
"-", |
66 |
|
"CLX", |
70 |
|
"EEX", |
72 |
|
"CHS", |
73 |
|
"ENTER^ |
76 |
|


