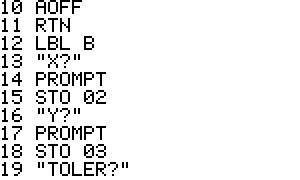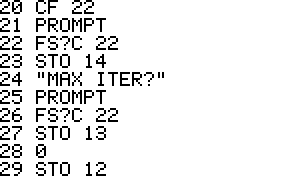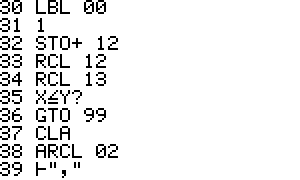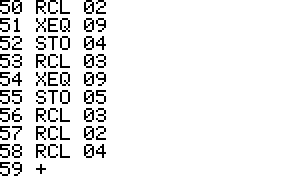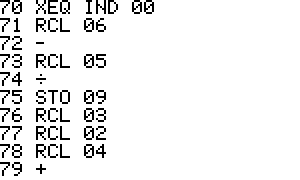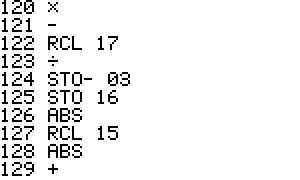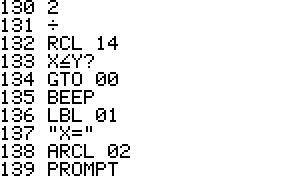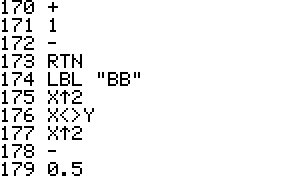Back to index
Roots2Eqns - find the roots of two nonlinear functions for the HP-42S
By Namir Shammas
Roots2Eqns is a program that finds the roots of 2 nonlinear functions. The program
uses a straightforward version of Newton's algorithm:
x' = x - [F Gy - G Fy] / J
y' = y - [G Fx - F Gy] / J
Where J = Fx Gy - Gx Fy
And,
F is F(x,y)
G is G(x,y)
Fx is dF(x,y)/dx
Gx is dG(x,y)/dx
Fy is dF(x,y)/dy
Gy is dG(x,y)/dy
The program approximates the first derivatives of the functions. For example:
dF(x,y)/dx = [F(x + hx, y) - F(x, y)] / hx
where hx = 0.01 * (1 + Abs(x))
And,
dF(x,y)/dy = [F(x, y + hy) - F(x, y)] / hy
where hy = 0.01 * (1 + Abs(y))
Usage:
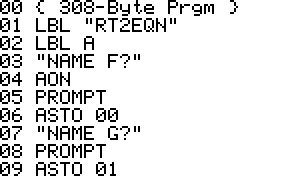
- To start the program execute XEQ "RT2EQN"
- The program prompts you for the names of the function F(x,y) and G(x,y) in Alpha mode.
- To find the roots, execute XEQ B and respond to the prompts for the
guesses, maximum number of iterations, and tolerance. The program will
iterate and display the root, function values at the root, and the
number of iterations.
- To select a new set of functions execute XEQ A and enter the new function names.
NOTE: To use previous values for maximum number of iterations and tolerance, simply
press the R/S key.
Example:
The label AA and BB implements the following sample functions:
F(x,y) = x^2 + y^2 - 1
G(x,y) = x^2 - y^2 + 0.5
Given F(x,y) and G(x,y) find the roots near x = 0.1 and y = 0.3
Allow 55 iterations at most and use a tolerance of 1E-7.
XEQ "RT2EQN"
NAME F?
AA
RUN
NAME G?
BB
RUN
XEQ B
X?
0.10000 RUN
Y?
0.30000 RUN
TOLER?
1E-7 RUN
MAX ITER?
55.00000 RUN
0.10000,0.30000
1.23744,1.37667
0.72437,0.96429
0.53698,0.87197
0.50178,0.86611
0.50003,0.86603
0.50000,0.86603
0.50000,0.86603
X=0.50000
RUN
Y=0.86603
RUN
F=6.58752E-9
RUN
G=6.23685E-9
RUN
ITERS=8.00000
The program found roots at x = 0.5 and y = 0.866.
Technical Notes:
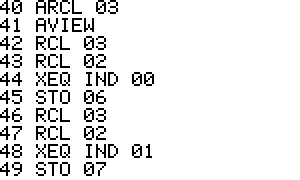
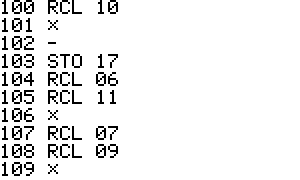
Memory usage:
R00 = Function name for F(x,y)
R01 = Function name for G(x,y)
R02 = x
R03 = y
R04 = hx (increment used to calculate the derivatives with respect to x)
R05 = hy (increment used to calculate the derivatives with respect to y)
R06 = F(x,y)
R07 = G(x,y)
R08 = dF/dx
R09 = dF/dy
R10 = dG/dx
R11 = dG/dy
R12 = Iters
R13 = Max Iters
R14 = Tolerance
R15 = Delta x
R16 = Delta y
R17 = J matrix
Label usage:
RT2EQN Main program label
AA Sample function F(x,y) label
BB Sample function G(x,y) label
A Supply function names
B Calculate root
00 Main loop
01 Show results
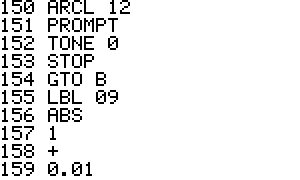
09 Calculate hx or hy
99 Display diverge message
Binary files for emulators:
Raw binary: roots2eqns.raw Binary for HP-42X: roots2eqns.42x (HP-48) roots2eqns49.42x (HP-49)
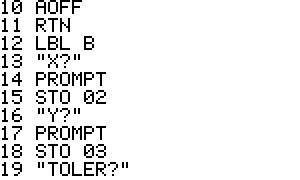
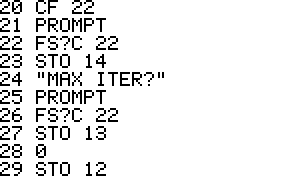
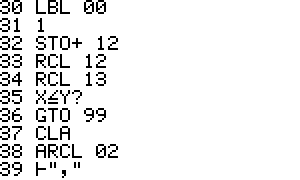
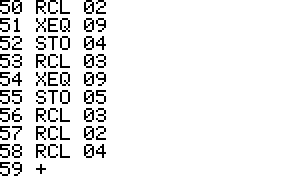

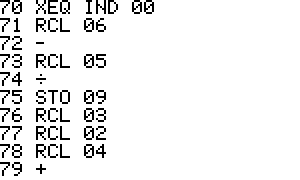



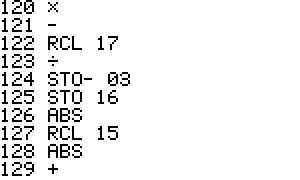
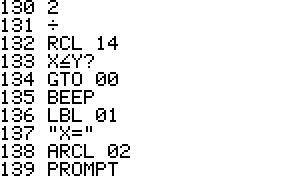


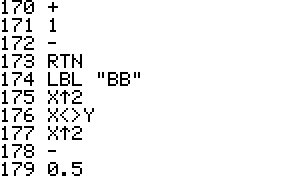

Generated by 42s2html - 10 May 2005, 20:01