
+- HP Forums (https://archived.hpcalc.org/museumforum)
+-- Forum: HP Museum Forums (https://archived.hpcalc.org/museumforum/forum-1.html)
+--- Forum: Old HP Forum Archives (https://archived.hpcalc.org/museumforum/forum-2.html)
+--- Thread: Why hyperbolic functions are critical ! (/thread-168347.html)
Why hyperbolic functions are critical ! - Gene Wright - 06-04-2010
TI had them. HP's did not.
In this case, TI was correct. Hyperbolic functions were critical to avoiding doom!
I saw this while watching the classic 1951 movie "The day the earth stood still" recently, which if you haven't seen, you should.
Professor Barnhardt's blackboard has equations written all over it that are critical for humanity to solve to get into space. Klaatu gives him a helping hand.
The equations definitely show hyperbolic trig functions. I had never noticed them until this time. Below is a picture of the blackboard, but it is too blurry to show the equations well...but they are there!
Anyone find a better picture or have the DVD to capture a frame to show?
:-) Who knew?
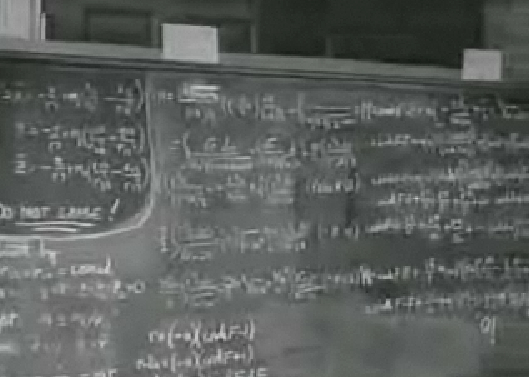
Re: Why hyperbolic functions are critical ! - Namir - 06-04-2010
And if we can calculate hyperbolic functions (and inverses) using an HP12C, then all is good in the land!
:->
Namir
Re: Why hyperbolic functions are critical ! - Ken Shaw - 06-04-2010
I vaguely recollect that the top left part of the blackboard has some equations that you would expect to find in an introductory calculus course, not on a scientist's blackboard! (OTOH, they are at least valid equations, IIRC.)
But I have the DVD. I'll see if I can grab a useful frame for you.
Re: Why hyperbolic functions are critical ! - Gene Wright - 06-07-2010
Here are the screen shots from the DVD courtesy of Ken. Thank you!
As I said, hyperbolic functions were critical to avoiding destruction of the human race in 1951. TI may have simply been trying to make sure we continued to survive! Why wasn't HP interested? lol. :-)



Re: Why hyperbolic functions are critical ! - Don Shepherd - 06-07-2010
Gene, I think the key to the survival of the earth is found in the first picture of your post. Bottom right corner: 0! and 0!! and 0!!!!?
If we can find a way of logically explaining to students why 0! = 1, then we will have the capacity to figure out how to survive as a species. And if can explain double-factorial and quadruple-factorial, we will indeed be the supreme species!
Re: Why hyperbolic functions are critical ! - Gene Wright - 06-07-2010
Lol
I'm not sure that's intended to be 0 factorial, etc, but surprise that the term turns out to BE zero.
Love this movie.
Re: Why hyperbolic functions are critical ! - Norman Dziedzic - 06-07-2010
You missed the " before each term so we actually need to figure out the double derivative of the quad-factorial of 0. <hmmm>
Re: Why hyperbolic functions are critical ! - Walter B - 06-07-2010
Look like equal signs to me, pointing to northwest or southeast :->
Re: Why hyperbolic functions are critical ! - Gene Wright - 06-07-2010
lol.
I think it is an equals sign for the terms above it. The !!! are the surprise of Dr. Barnhardt that the terms were equal to 0.
Re: Why hyperbolic functions are critical ! - Gerson W. Barbosa - 06-07-2010
Yes, one of the terms appears to be
which is indeed equal to 0.5 / 1 7 1 \
F * | - ---- + ------ + ----- | ,
\ 6*3! 3*5! 5! /
Re: Why hyperbolic functions are critical ! - Martin Pinckney - 06-07-2010
What is "F" in the relations?
Re: Why hyperbolic functions are critical ! - Eric Smith - 06-08-2010
Quote:
If we can find a way of logically explaining to students why 0! = 1
Trivially.
(n+1)! = n! * (n+1), by the definition of factorial
n! = (n+1)! / (n+1)
2! = 3! / 3, and since 3! = 6, 2! = 2
1! = 2! / 2, and since 2! = 2, 1! = 1
0! = 1! / 1, and since 1! = 1, 0! = 1
One more step shows why (-1)! is undefined, and by extension, the factorial of any negative integers.
Quote:
then we will have the capacity to figure out how to survive as a species.
If only it were that easy!
Re: Why hyperbolic functions are critical ! - Gerson W. Barbosa - 06-08-2010
I don't have the foggiest notion ... By the way, does anyone know if those equations have a meaning at all?
Re: Why hyperbolic functions are critical ! - Ken Shaw - 06-09-2010
In an interview, Robert Wise (the film director) said they hired an academic to write a problem in orbital mechanics on the board (or words to that effect).
There's something like it here (link).
Re: Why hyperbolic functions are critical ! - Martin Pinckney - 06-09-2010
Turns out "F" is the "hyperbolic eccentric anomaly". This is clearly explained in Spacecraft Systems Engineering
By Peter W. Fortescue, John Stark, and Graham Swinerd.