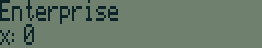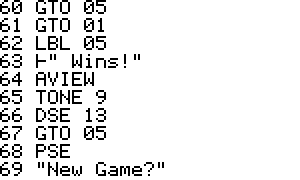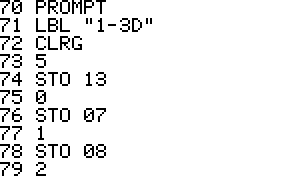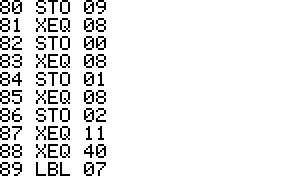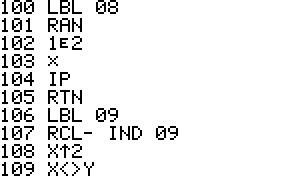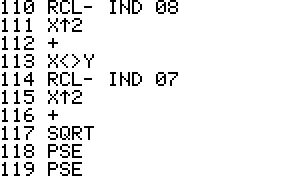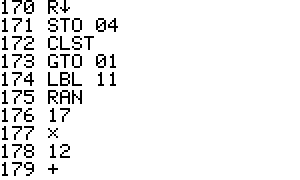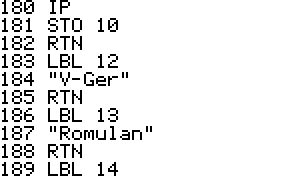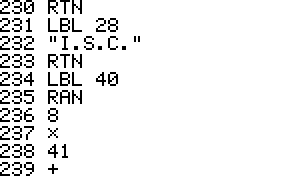Back to index
Trek for the HP-42S
By Richard Garner
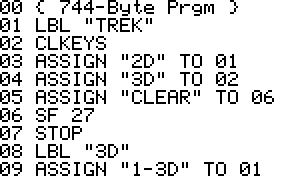
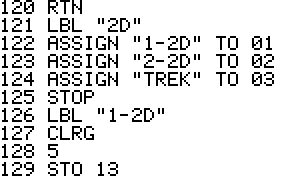
Trek is a Star Trek game for the HP-42S. It contains a 2D and 3D
version that can be played by 1 or 2 players.
Example:
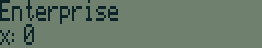
Usage:
The playing field is either a square 100x100 in size or a cube
100x100x100 in size. The program will randomly select a main Star
Trek
ship. Enterprise, Enterprise A - E, Voyager, or Defiant. It will
then
randomly select from about 16 enemies.
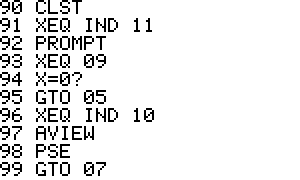
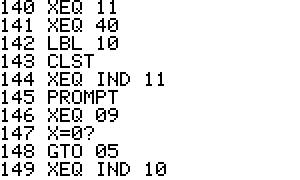
In the 1 player games the
calculator will randomly generate the coordinates of the enemy ship and
you enter in coordinates to fire at. The closer the readout is to Zero
the closer you are to destroying that ship. In the 2 player game that
calculator stops and requests each player to enter the coordinates of
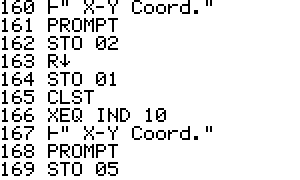
their ship before the game starts. To enter coordinates, load the
stack with your numbers. Enter the X then the Y then Z assuming the 3D
game is chosen, then press R/S. To fire at your enemy do the same.
Enter the X then the Y then the Z coordinates you wish to fire upon and
press R/S. The number that is returned to the screen will indicate how
close you are tohitting your target. The closer to Zero the number is
the closer you are to destroying them.
Binary files for emulators:
Raw binary: trek.raw Binary for
HP-42X: trek.42x State-file for
Emu42
(ROM Rev C.): trek.e42

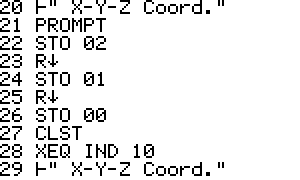

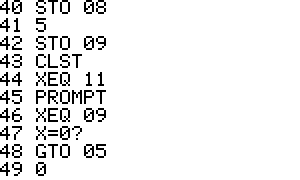
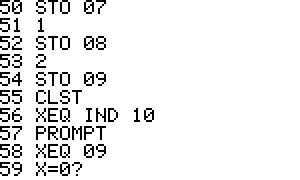
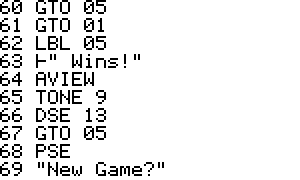
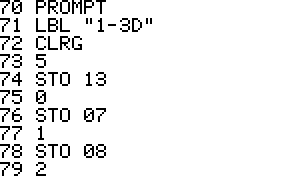
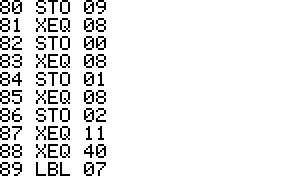
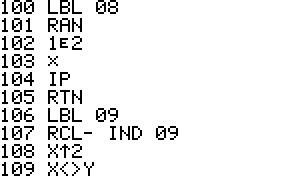
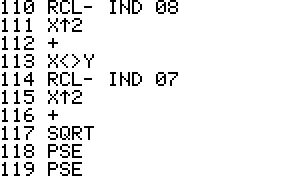


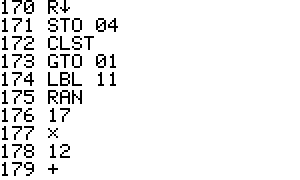



Generated by 42s2html - 05
June 2004, 23:36