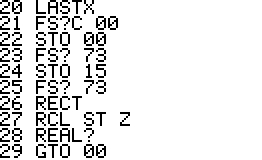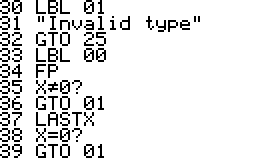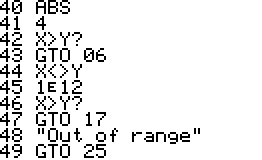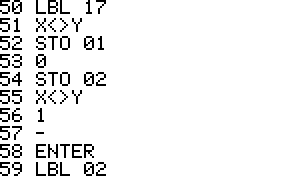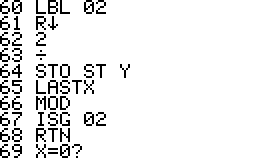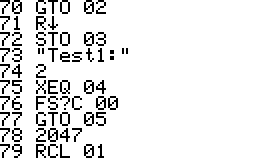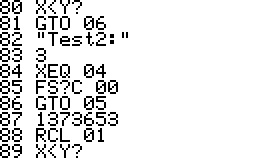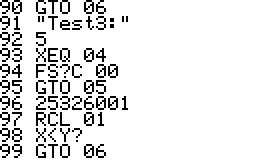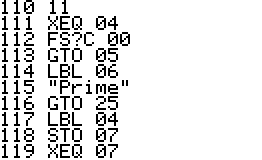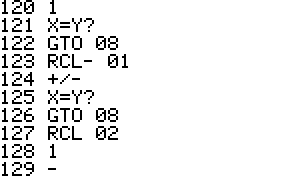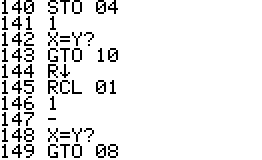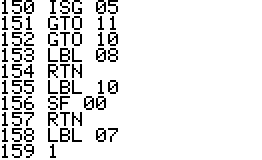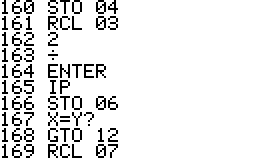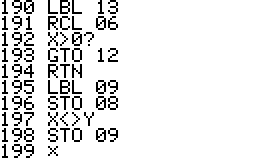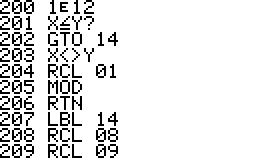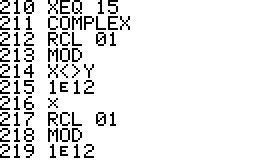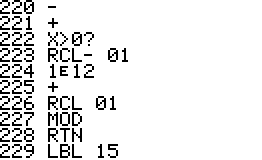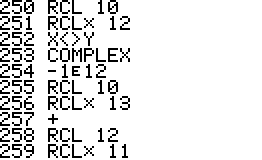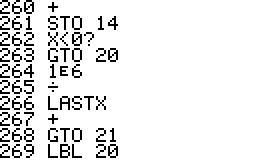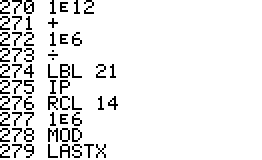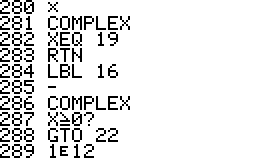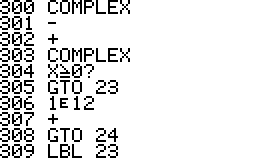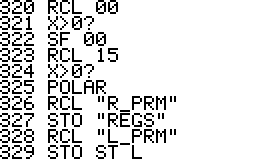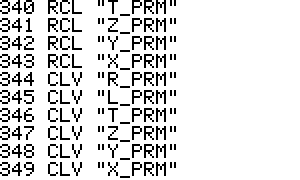Back to index
Miller-Rabin Primality Test for the HP-42S
By Erik
Ehrling
(Sweden) with a fix by J F Garnier. Any comments or suggestions are
very welcome!
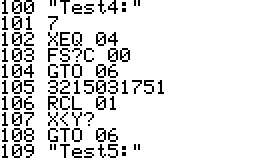
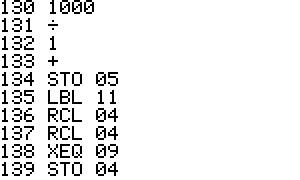
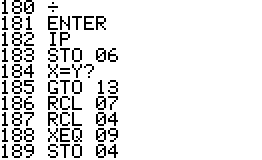
This is an implementation of the Miller-Rabin primality test for the
HP42S. Given an integer as input it returns whether it s a prime number
or a composite of several factors.
Usage:
Using PRM? is simple, just enter an integer 1 to 999 999 999 999
and run PRM?. Depending on the size of the integer the running time can
be anything from a few seconds up to five minutes for a very large
primes. The program goes through a number of "rounds" in which the
number is tested for primality. If a test fails then all the following
rounds are skipped, on the other hand a prime is not claimed a prime
until it has passed all rounds. For a small integer one round is
sufficient, while larger integers require up to five rounds.
When the test is finished the result (Composite or Prime) will be
displayed in the
upper area of the LCD and can also be found in the alpha register.
Note that the stack, all numbered registers and user flags are left
unaltered by the program. It is therefore possible to run PRM? in the
middle of a calculation and then continue after it has run.
Examples:
Technical notes:
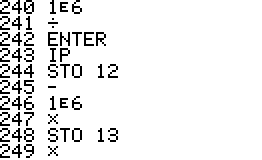
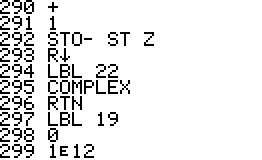
- The program is implemented using a repeated square-and-multiply
algorithm for exponentiation. To handle a * b mod n for large a,b,n the
program uses a partial implementation of addition and
multiplication of double precision integers which are represented
internally as complex
numbers.
- Slightly updated wrapper for program encapsulation now also
supports complex registers (REGS) when running PRM?
- The variables X_PRM, Y_PRM, Z_PRM, T_PRM, L_PRM,
R_PRM are used for storing stack and register contents and should
be considered reserved variables
References:
For a good description of the Miller-Rabin algorithm see
Menezes et al., "Handbook
of Applied Cryptography", p 71 [paragraph 2.143] and p 139f [paragraph
2.4].
Binary files for emulators:
Raw binary: prm.raw Binary for
HP-42X: prm.42x
Revision History:
1.01 - Fixed errors which caused unreliable results for large n.
Thanks to J F Garnier for both pointing out and providing the fix for
this problem!


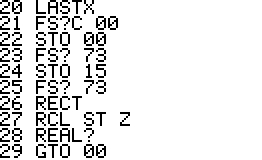
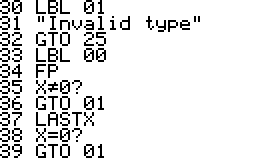
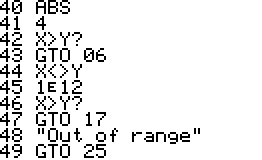
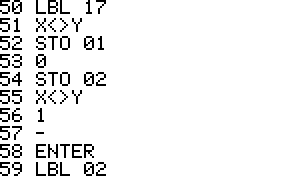
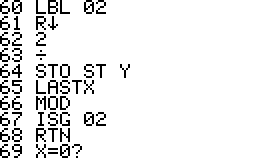
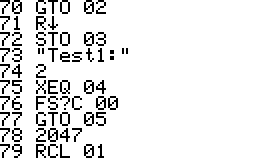
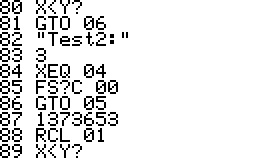
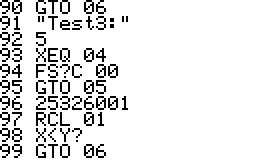
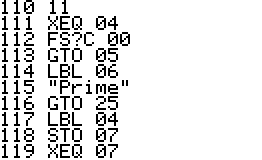
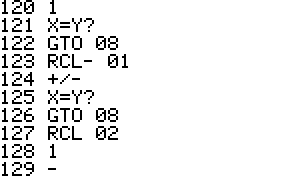
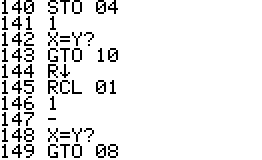
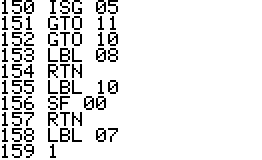
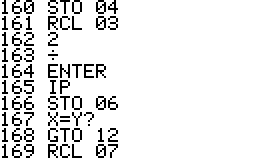

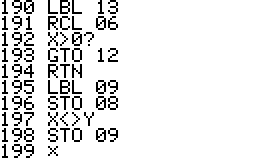
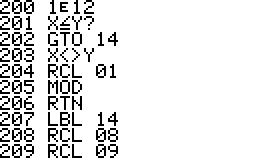
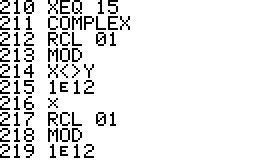
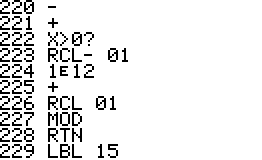

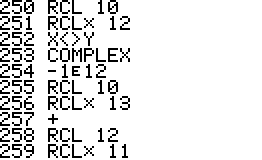
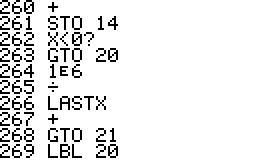
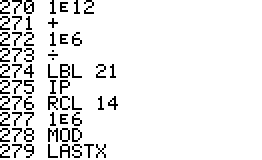
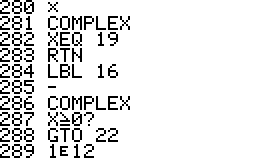
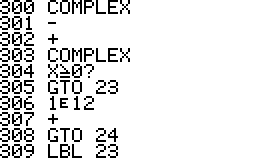

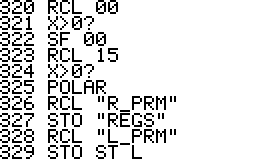

Generated by 42s2html - 19
September 2004, 17:21